Difference between revisions of "Python:Ordinary Differential Equations/Examples"
| Line 2: | Line 2: | ||
== Examples == | == Examples == | ||
| − | Note - each example began with the [[MATLAB:Ordinary Differential Equations/Templates|Templates]] provided at this web site. Some comments have been removed from the templates to conserve space while some comments may have been added to provide a clearer explanation of the process for a particular example. | + | Note - each example began with the [[MATLAB:Ordinary Differential Equations/Templates|Templates]] provided at this web site. Some comments have been removed from the templates to conserve space while some comments may have been added to provide a clearer explanation of the process for a particular example. They all assume a file called <code>ode_helpers.py</code> that contains the code is in the same folder as the example codes: |
| + | <syntaxhighlight lang='python'> | ||
| + | import numpy as np | ||
| + | import matplotlib.pyplot as plt | ||
| + | |||
| + | def state_plotter(times, states, fig_num): | ||
| + | num_states = np.shape(states)[0] | ||
| + | num_cols = int(np.ceil(np.sqrt(num_states))) | ||
| + | num_rows = int(np.ceil(num_states / num_cols)) | ||
| + | f, ax = plt.subplots(num_rows, num_cols, num=fig_num, clear=True, | ||
| + | squeeze=False) | ||
| + | for n in range(num_states): | ||
| + | row = n // num_cols | ||
| + | col = n % num_cols | ||
| + | ax[row][col].plot(times, states[n], 'k.:') | ||
| + | ax[row][col].set(xlabel='Time', | ||
| + | ylabel='$y_{:0.0f}(t)$'.format(n), | ||
| + | title='$y_{:0.0f}(t)$ vs. Time'.format(n)) | ||
| + | f.tight_layout() | ||
| + | for n in range(num_states, num_rows * num_cols): | ||
| + | f.delaxes(ax[n // num_cols][n % num_cols]) | ||
| + | </syntaxhighlight> | ||
=== Constant Rate of Change === | === Constant Rate of Change === | ||
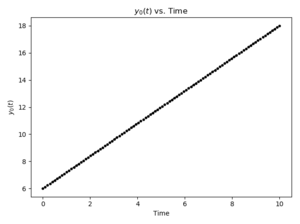
| − | [[File: | + | [[File:ODEConstDiffPlot_p.png|thumb|Result using constant rate of change.]] |
If the dependent variable has a constant rate of change: | If the dependent variable has a constant rate of change: | ||
<center><math> | <center><math> | ||
| Line 11: | Line 32: | ||
</math></center> | </math></center> | ||
where <math>C</math> is some constant, you can provide the differential equation | where <math>C</math> is some constant, you can provide the differential equation | ||
| − | + | in the <code>f</code> function and then calculate answers using this model with the code below. | |
| − | + | The code assumes there are 100 evenly spaced times between 0 and 10, the | |
| − | function | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
initial value of <math>y</math> is 6, and the rate of change is 1.2: | initial value of <math>y</math> is 6, and the rate of change is 1.2: | ||
| − | < | + | <syntaxhighlight lang="python"> |
| − | % | + | # %% Imports |
| − | + | import numpy as np | |
| − | + | import matplotlib.pyplot as plt | |
| − | + | from scipy.integrate import solve_ivp | |
| − | + | from ode_helpers import state_plotter | |
| − | % | + | # %% Define independent function and derivative function |
| − | + | def f(t, y, c): | |
| − | + | dydt = [c[0]] | |
| − | + | return dydt | |
| − | |||
| − | % | + | # %% Define time spans, initial values, and constants |
| − | + | tspan = np.linspace(0, 10, 100) | |
| + | yinit = [6] | ||
| + | c = [1.2] | ||
| − | %% | + | # %% Solve differential equation |
| − | + | sol = solve_ivp(lambda t, y: f(t, y, c), | |
| − | + | [tspan[0], tspan[-1]], yinit, t_eval=tspan) | |
| − | [ | ||
| − | % Plot | + | # %% Plot states |
| − | + | state_plotter(sol.t, sol.y, 1) | |
| − | + | </syntaxhighlight > | |
| − | |||
| − | |||
| − | </ | ||
===Time-dependent Rate of Change=== | ===Time-dependent Rate of Change=== | ||
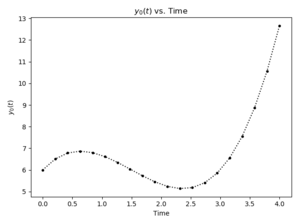
| − | [[File: | + | [[File:ODETimeDiffPlot_p.png|thumb|Result using time-varying rate of change]] |
If the dependent variable's rate of change is some function of time, | If the dependent variable's rate of change is some function of time, | ||
| − | this can be easily | + | this can be easily coded. For example, if the |
differential equation is some quadratic function given as: | differential equation is some quadratic function given as: | ||
<center><math> | <center><math> | ||
| Line 65: | Line 71: | ||
</math></center> | </math></center> | ||
then the function providing the values of the derivative may be | then the function providing the values of the derivative may be | ||
| − | written | + | written using <code>np.polyval</code>. |
| − | + | You could calculate answers using this model with the following code; | |
| − | + | it assumes there are 20 evenly spaced times between 0 and 4, the | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | You could calculate answers using this model with the following code | ||
| − | |||
| − | |||
initial value of <math>y</math> is 6, and the polynomial is defined by the vector | initial value of <math>y</math> is 6, and the polynomial is defined by the vector | ||
| − | [2 -6 3]: | + | [2, -6, 3]: |
| − | < | + | <syntaxhighlight lang="python"> |
| − | % | + | # %% Imports |
| − | + | import numpy as np | |
| + | import matplotlib.pyplot as plt | ||
| + | from scipy.integrate import solve_ivp | ||
| + | from ode_helpers import state_plotter | ||
| − | % | + | # %% Define derivative function |
| − | + | def f(t, y, c): | |
| + | dydt = np.polyval(c, t) | ||
| + | return dydt | ||
| + | |||
| + | # %% Define time spans, initial values, and constants | ||
| + | tspan = np.linspace(0, 4, 20) | ||
| + | yinit = [6] | ||
| + | c = [2, -6, 3] | ||
| − | % | + | # %% Solve differential equation |
| − | + | sol = solve_ivp(lambda t, y: f(t, y, c), | |
| − | tspan | + | [tspan[0], tspan[-1]], yinit, t_eval=tspan) |
| − | yinit = | ||
| − | |||
| − | % | + | # %% Plot states |
| − | + | state_plotter(sol.t, sol.y, 1) | |
| − | + | </syntaxhighlight > | |
| − | % | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | </ | ||
===Population Growth=== | ===Population Growth=== | ||
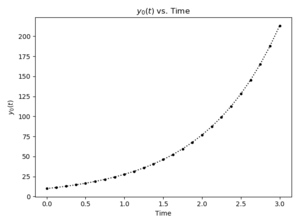
| − | [[File: | + | [[File:ODEPopDiffPlot_p.png|thumb|Result using rate of change proportional to measurement]] |
For population growth, the rate of change of population is dependent | For population growth, the rate of change of population is dependent | ||
upon the number of people as well as some constant of | upon the number of people as well as some constant of | ||
| Line 119: | Line 112: | ||
</math></center> | </math></center> | ||
where <math>C</math> is again some constant. | where <math>C</math> is again some constant. | ||
| − | + | The following code will calculate the population for a span of 3 seconds with 25 | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | The following code | ||
| − | a span of 3 seconds with 25 | ||
points for the population model above with an initial population of 10 | points for the population model above with an initial population of 10 | ||
and a constant of proportionality of 1.02: | and a constant of proportionality of 1.02: | ||
| − | < | + | <syntaxhighlight lang="python"> |
| − | % | + | # %% Imports |
| − | + | import numpy as np | |
| − | + | import matplotlib.pyplot as plt | |
| − | % | + | from scipy.integrate import solve_ivp |
| − | + | from ode_helpers import state_plotter | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | % | + | # %% Define derivative function |
| − | + | def f(t, y, c): | |
| + | dydt = [c[0] * y[0]] | ||
| + | return dydt | ||
| + | |||
| + | # %% Define time spans, initial values, and constants | ||
| + | tspan = np.linspace(0, 3, 25) | ||
| + | yinit = [10] | ||
| + | c = [1.02] | ||
| − | %% | + | # %% Solve differential equation |
| − | + | sol = solve_ivp(lambda t, y: f(t, y, c), | |
| − | + | [tspan[0], tspan[-1]], yinit, t_eval=tspan) | |
| − | [ | ||
| − | % Plot | + | # %% Plot states |
| − | + | state_plotter(sol.t, sol.y, 1) | |
| − | + | </syntaxhighlight> | |
| − | |||
| − | </ | ||
===Multiple Variable Models=== | ===Multiple Variable Models=== | ||
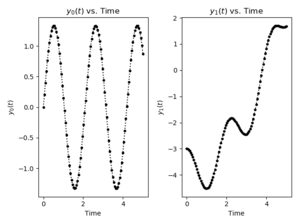
| − | [[File: | + | [[File:ODETwoDiffPlot_p.png|thumb|Result for system with two variables]] |
It is possible to solve multiple-variable systems by making sure the | It is possible to solve multiple-variable systems by making sure the | ||
| Line 172: | Line 151: | ||
<center><math> | <center><math> | ||
\begin{align} | \begin{align} | ||
| − | \frac{ | + | \frac{dy_0}{dt}&=\alpha\cos(\beta t) & |
| − | \frac{ | + | \frac{dy_1}{dt}&=\gamma y_0+\delta t |
\end{align} | \end{align} | ||
</math></center> | </math></center> | ||
| − | The differential | + | The differential function <code>f</code> for this system will have a 2 element list as the output. |
| − | + | Also, if you have systems with multiple dependent variables, just | |
| − | + | be sure to put the initial conditions in a list. For | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | be sure to put the initial conditions in a | ||
example, with the system defined as: | example, with the system defined as: | ||
<center><math> | <center><math> | ||
\begin{align} | \begin{align} | ||
| − | \frac{ | + | \frac{dy_0}{dt}&=4\cos(3t) & |
| − | \frac{ | + | \frac{dy_1}{dt}&=-2y_1+0.5t |
\end{align} | \end{align} | ||
</math></center> | </math></center> | ||
| − | you could use the following script | + | you could use the following script to solve for both |
| − | <math> | + | <math>y_0</math> and <math>y_1</math>; the code assumes <math>y_0</math> starts as 0 and <math>y_1</math> starts at -3: |
| − | < | + | <syntaxhighlight lang="python"> |
| − | % | + | # %% Imports |
| − | + | import numpy as np | |
| + | import matplotlib.pyplot as plt | ||
| + | from scipy.integrate import solve_ivp | ||
| + | from ode_helpers import state_plotter | ||
| − | % | + | # %% Define derivative function |
| − | + | def f(t, y, c): | |
| + | dydt = [c[0]*np.cos(c[1]*t), c[2]*y[0]+c[3]*t] | ||
| + | return dydt | ||
| − | % | + | # %% Define time spans, initial values, and constants |
| − | + | tspan = np.linspace(0, 5, 100) | |
| − | tspan = linspace(0, 5) | + | yinit = [0, -3] |
| − | yinit = [0 -3] | + | c = [4, 3, -2, 0.5] |
| − | |||
| − | % | + | # %% Solve differential equation |
| − | + | sol = solve_ivp(lambda t, y: f(t, y, c), | |
| + | [tspan[0], tspan[-1]], yinit, t_eval=tspan) | ||
| − | %% | + | # %% Plot states |
| − | + | state_plotter(sol.t, sol.y, 1) | |
| − | + | </syntaxhighlight> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | </ | ||
=== Higher Order Differential Equations === | === Higher Order Differential Equations === | ||
| − | [[File: | + | [[File:ODEJerkDiffPlot_p.png|thumb|Result using constant third derivative.]] |
The system must be written in terms of first-order | The system must be written in terms of first-order | ||
differential equations only. To solve a system with | differential equations only. To solve a system with | ||
higher-order derivatives, you will first write a cascading system of simple | higher-order derivatives, you will first write a cascading system of simple | ||
| − | first-order equations then use them in your differential | + | first-order equations then use them in your differential function. For |
example, assume you have a system characterized by constant jerk: | example, assume you have a system characterized by constant jerk: | ||
<center><math> | <center><math> | ||
| Line 245: | Line 208: | ||
<center><math> | <center><math> | ||
\begin{align} | \begin{align} | ||
| − | + | y_0 &=y &~& &~\\ | |
| − | \frac{ | + | \frac{dy_0}{dt}&=\frac{dy}{dt}=y_1 & &\longrightarrow & \frac{dy_0}{dt}&=y_1\\ |
| − | \frac{ | + | \frac{dy_1}{dt}&=\frac{d^2y_0}{dt^2}=\frac{d^2y}{dt^2}=y_2 & &\longrightarrow & |
| − | \frac{ | + | \frac{dy_1}{dt}&=y_2\\ |
| − | \frac{ | + | \frac{dy_2}{dt}&=\frac{d^2y_1}{dt^2}=\frac{d^3y_0}{dt^3}=\frac{d^3y}{dt^3}=j=C & |
&\longrightarrow & | &\longrightarrow & | ||
| − | \frac{ | + | \frac{dy_2}{dt}&=C |
\end{align}</math></center> | \end{align}</math></center> | ||
Notice how the derivatives cascade so that the constant jerk equation | Notice how the derivatives cascade so that the constant jerk equation | ||
| − | can now be written as a set of three first-order equations. | + | can now be written as a set of three first-order equations. Note that in this system, |
| − | + | <code>y[0]</code> represents the position, <code>y[1]</code> represents the velocity, and | |
| − | + | <code>y[2]</code> represents the acceleration. This type of cascading system will | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | < | ||
| − | < | ||
show up often when modeling equations of motion. | show up often when modeling equations of motion. | ||
| Line 277: | Line 226: | ||
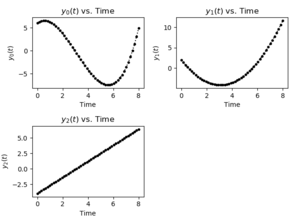
position of 6, and initial velocity of 2, an initial acceleration of | position of 6, and initial velocity of 2, an initial acceleration of | ||
-4, and a constant jerk of 1.3: | -4, and a constant jerk of 1.3: | ||
| − | < | + | <syntaxhighlight lang='python'> |
| − | + | # %% Imports | |
| − | + | import numpy as np | |
| − | + | import matplotlib.pyplot as plt | |
| − | % | + | from scipy.integrate import solve_ivp |
| − | % | + | from ode_helpers import state_plotter |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | %% | + | # %% Define derivative function |
| − | + | def f(t, y, c): | |
| − | + | dydt = [y[1], y[2], c[0]] | |
| − | [ | + | return dydt |
| − | % | + | # %% Define time spans, initial values, and constants |
| − | + | tspan = np.linspace(0, 8, 50) | |
| − | + | yinit = [6, 2, -4] | |
| − | + | c = [1.3] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | # %% Solve differential equation | |
| + | sol = solve_ivp(lambda t, y: f(t, y, c), | ||
| + | [tspan[0], tspan[-1]], yinit, t_eval=tspan) | ||
| − | + | # %% Plot states | |
| − | + | state_plotter(sol.t, sol.y, 1) | |
| − | + | </syntaxhighlight> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | </ | ||
== Questions == | == Questions == | ||
Revision as of 22:37, 26 November 2018
The following examples show different ways of setting up and solving initial value problems in Python. It is part of the page on Ordinary Differential Equations in Python and is very much based on MATLAB:Ordinary Differential Equations/Examples.
Contents
Examples
Note - each example began with the Templates provided at this web site. Some comments have been removed from the templates to conserve space while some comments may have been added to provide a clearer explanation of the process for a particular example. They all assume a file called ode_helpers.py that contains the code is in the same folder as the example codes:
import numpy as np
import matplotlib.pyplot as plt
def state_plotter(times, states, fig_num):
num_states = np.shape(states)[0]
num_cols = int(np.ceil(np.sqrt(num_states)))
num_rows = int(np.ceil(num_states / num_cols))
f, ax = plt.subplots(num_rows, num_cols, num=fig_num, clear=True,
squeeze=False)
for n in range(num_states):
row = n // num_cols
col = n % num_cols
ax[row][col].plot(times, states[n], 'k.:')
ax[row][col].set(xlabel='Time',
ylabel='$y_{:0.0f}(t)$'.format(n),
title='$y_{:0.0f}(t)$ vs. Time'.format(n))
f.tight_layout()
for n in range(num_states, num_rows * num_cols):
f.delaxes(ax[n // num_cols][n % num_cols])
Constant Rate of Change
If the dependent variable has a constant rate of change:
where \(C\) is some constant, you can provide the differential equation
in the f function and then calculate answers using this model with the code below.
The code assumes there are 100 evenly spaced times between 0 and 10, the
initial value of \(y\) is 6, and the rate of change is 1.2:
# %% Imports
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp
from ode_helpers import state_plotter
# %% Define independent function and derivative function
def f(t, y, c):
dydt = [c[0]]
return dydt
# %% Define time spans, initial values, and constants
tspan = np.linspace(0, 10, 100)
yinit = [6]
c = [1.2]
# %% Solve differential equation
sol = solve_ivp(lambda t, y: f(t, y, c),
[tspan[0], tspan[-1]], yinit, t_eval=tspan)
# %% Plot states
state_plotter(sol.t, sol.y, 1)
Time-dependent Rate of Change
If the dependent variable's rate of change is some function of time, this can be easily coded. For example, if the differential equation is some quadratic function given as:
then the function providing the values of the derivative may be
written using np.polyval.
You could calculate answers using this model with the following code;
it assumes there are 20 evenly spaced times between 0 and 4, the
initial value of \(y\) is 6, and the polynomial is defined by the vector
[2, -6, 3]:
# %% Imports
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp
from ode_helpers import state_plotter
# %% Define derivative function
def f(t, y, c):
dydt = np.polyval(c, t)
return dydt
# %% Define time spans, initial values, and constants
tspan = np.linspace(0, 4, 20)
yinit = [6]
c = [2, -6, 3]
# %% Solve differential equation
sol = solve_ivp(lambda t, y: f(t, y, c),
[tspan[0], tspan[-1]], yinit, t_eval=tspan)
# %% Plot states
state_plotter(sol.t, sol.y, 1)
Population Growth
For population growth, the rate of change of population is dependent upon the number of people as well as some constant of proportionality:
where \(C\) is again some constant. The following code will calculate the population for a span of 3 seconds with 25 points for the population model above with an initial population of 10 and a constant of proportionality of 1.02:
# %% Imports
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp
from ode_helpers import state_plotter
# %% Define derivative function
def f(t, y, c):
dydt = [c[0] * y[0]]
return dydt
# %% Define time spans, initial values, and constants
tspan = np.linspace(0, 3, 25)
yinit = [10]
c = [1.02]
# %% Solve differential equation
sol = solve_ivp(lambda t, y: f(t, y, c),
[tspan[0], tspan[-1]], yinit, t_eval=tspan)
# %% Plot states
state_plotter(sol.t, sol.y, 1)
Multiple Variable Models
It is possible to solve multiple-variable systems by making sure the differential function returns values for each of the variables. For instance, in the following system the first variable's rate of change depends only on time while the second is dependent upon both time and the first variable:
The differential function f for this system will have a 2 element list as the output.
Also, if you have systems with multiple dependent variables, just
be sure to put the initial conditions in a list. For
example, with the system defined as:
you could use the following script to solve for both \(y_0\) and \(y_1\); the code assumes \(y_0\) starts as 0 and \(y_1\) starts at -3:
# %% Imports
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp
from ode_helpers import state_plotter
# %% Define derivative function
def f(t, y, c):
dydt = [c[0]*np.cos(c[1]*t), c[2]*y[0]+c[3]*t]
return dydt
# %% Define time spans, initial values, and constants
tspan = np.linspace(0, 5, 100)
yinit = [0, -3]
c = [4, 3, -2, 0.5]
# %% Solve differential equation
sol = solve_ivp(lambda t, y: f(t, y, c),
[tspan[0], tspan[-1]], yinit, t_eval=tspan)
# %% Plot states
state_plotter(sol.t, sol.y, 1)
Higher Order Differential Equations
The system must be written in terms of first-order differential equations only. To solve a system with higher-order derivatives, you will first write a cascading system of simple first-order equations then use them in your differential function. For example, assume you have a system characterized by constant jerk:
The first thing to do is write three first-order differential equations to represent the third-order equation:
Notice how the derivatives cascade so that the constant jerk equation
can now be written as a set of three first-order equations. Note that in this system,
y[0] represents the position, y[1] represents the velocity, and
y[2] represents the acceleration. This type of cascading system will
show up often when modeling equations of motion.
The following script, RunJerkDiff.m, calculates the position,
velocity, and speed over a period of 8 seconds assuming an initial
position of 6, and initial velocity of 2, an initial acceleration of
-4, and a constant jerk of 1.3:
# %% Imports
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp
from ode_helpers import state_plotter
# %% Define derivative function
def f(t, y, c):
dydt = [y[1], y[2], c[0]]
return dydt
# %% Define time spans, initial values, and constants
tspan = np.linspace(0, 8, 50)
yinit = [6, 2, -4]
c = [1.3]
# %% Solve differential equation
sol = solve_ivp(lambda t, y: f(t, y, c),
[tspan[0], tspan[-1]], yinit, t_eval=tspan)
# %% Plot states
state_plotter(sol.t, sol.y, 1)
Questions
Post your questions by editing the discussion page of this article. Edit the page, then scroll to the bottom and add a question by putting in the characters *{{Q}}, followed by your question and finally your signature (with four tildes, i.e. ~~~~). Using the {{Q}} will automatically put the page in the category of pages with questions - other editors hoping to help out can then go to that category page to see where the questions are. See the page for Template:Q for details and examples.