Difference between revisions of "EGR 103/Concept List/F21"
Jump to navigation
Jump to search
\(
y=e^x=\sum_{n=0}^{\infty}\frac{x^n}{n!}
\)
\(
\begin{align}
y_{init}&=1\\
y_{new}&=y_{old}+\frac{x^n}{n!}
\end{align}
\)
| Line 166: | Line 166: | ||
</math> | </math> | ||
* See Python version of Fig. 4.2 and modified version of 4.2 in the Resources section of Sakai page under Chapra Pythonified | * See Python version of Fig. 4.2 and modified version of 4.2 in the Resources section of Sakai page under Chapra Pythonified | ||
| + | |||
| + | == Lecture 10 - Binary == | ||
| + | * Different number systems convey information in different ways. | ||
| + | ** Roman Numerals | ||
| + | ** Chinese Numbers | ||
| + | ** Binary Numbers | ||
| + | *** We went through how to convert between decimal and binary | ||
| + | * Floats (specifically double precision floats) are stored with a sign bit, 52 fractional bits, and 11 exponent bits. The exponent bits form a code: | ||
| + | ** 0 (or 00000000000): the number is either 0 or a denormal | ||
| + | ** 2047 (or 11111111111): the number is either infinite or not-a-number | ||
| + | ** Others: the power of 2 for scientific notation is 2**(code-1023) | ||
| + | *** The largest number is thus just *under* 2**1024 (ends up being (2-2**-52)**1024<math>\approx 1.798\times 10^{308}</math>. | ||
| + | *** The smallest normal number (full precision) is 2**(-1022)<math>\approx 2.225\times 10^{-308}</math>. | ||
| + | *** The smallest denormal number (only one significant binary digit) is 2**(-1022)/2**53 or 5e-324. | ||
| + | ** When adding or subtracting, Python can only operate on the common significant digits - meaning the smaller number will lose precision. | ||
| + | ** (1+1e-16)-1=0 and (1+1e-15)-1=1.1102230246251565e-15 | ||
| + | ** Avoid intermediate calculations that cause problems: if x=1.7e308, | ||
| + | *** (x+x)/x is inf | ||
| + | *** x/x + x/x is 2.0 | ||
| + | ** $$e^x=\lim_{n\rightarrow \infty}\left(1+\frac{x}{n}\right)^n$$ | ||
| + | <div class="mw-collapsible mw-collapsed"> | ||
| + | <source lang=python> | ||
| + | # Exponential Demo | ||
| + | </source> | ||
| + | <div class="mw-collapsible-content"> | ||
| + | <syntaxhighlightlang=python> | ||
| + | import numpy as np | ||
| + | import matplotlib.pyplot as plt | ||
| + | |||
| + | def exp_calc(x, n): | ||
| + | return (1 + x/n)**n | ||
| + | |||
| + | if __name__ == "__main__": | ||
| + | n = np.logspace(0, 17, 1000) | ||
| + | y = exp_calc(1, n) | ||
| + | fig, ax = plt.subplots(num=1, clear=True) | ||
| + | ax.semilogx(n, y) | ||
| + | fig.savefig('ExpDemoPlot1.png') | ||
| + | |||
| + | # Focus on right part | ||
| + | n = np.logspace(13, 16, 1000) | ||
| + | y = exp_calc(1, n) | ||
| + | fig, ax = plt.subplots(num=2, clear=True) | ||
| + | ax.semilogx(n, y) | ||
| + | fig.savefig('ExpDemoPlot2.png') | ||
| + | </syntaxhighlight> | ||
| + | </div> | ||
| + | </div> | ||
| + | <gallery> | ||
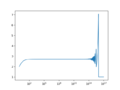
| + | File:ExpDemoPlot1.png|estimates for calculating $$e$$ with $$n$$ between 1 and $$1*10^{17}$$ | ||
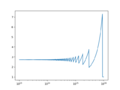
| + | File:ExpDemoPlot2.png|$$n$$ between $$10^{13}$$ and $$10^{16}$$ showing region when roundoff causes problems | ||
| + | </gallery> | ||
| + | |||
| + | * Want to see Amharic? | ||
| + | list(map(chr, range(4608, 4992))) | ||
| + | * Want to see the Greek alphabet? | ||
| + | <syntaxhighlight lang=python> | ||
| + | for k in range(913,913+25): | ||
| + | print(chr(k), chr(k+32)) | ||
| + | </syntaxhighlight> | ||
| + | |||
| + | == Lecture 11 - Monte Carlo Methods == | ||
| + | * From Wikipedia: [https://en.wikipedia.org/wiki/Monte_Carlo_method Monte Carlo method] | ||
| + | * Walker demo | ||
| + | <html><iframe src="https://trinket.io/embed/python3/e1a9a460b1" width="100%" height="600" frameborder="0" marginwidth="0" marginheight="0" allowfullscreen></iframe></html> | ||
Revision as of 15:56, 27 September 2021
Contents
- 1 Lecture 1 - Course Introduction
- 2 Lecture 2 - Programs and Programming
- 3 Lecture 3 - "Number" Types
- 4 Lecture 4 - Other Types
- 5 Lecture 5 - Format and Functions
- 6 Lecture 6 - Relational Operators, Decisions, and Loops
- 7 Lecture 7 - More Loops and Logical Masks
- 8 Lecture 8 - Dictionaries
- 9 Lecture 9 - Iterative Methods
- 10 Lecture 10 - Binary
- 11 Lecture 11 - Monte Carlo Methods
Lecture 1 - Course Introduction
- Main class page: EGR 103L.
- See information on PDF of slide show on Errata / Notes page.
- Sakai page: Sakai 103L page; grades, surveys and tests, some assignment submissions
- Pundit page: EGR 103; reference lists
- CampusWire page: CampusWire 103L page; message board for questions - you need to be in the class and have the access code 8018 to subscribe.
Lecture 2 - Programs and Programming
- Almost all languages have input, output, math, conditional execution (decisions), and repetition (loops)
- Seven steps of programming The Seven Steps Poster
- Watch video on Developing an Algorithm
- Watch video on A Seven Step Approach to Solving Programming Problems
- Consider how to decide if a number is a prime number
- To play with Python:
- Install it on your machine or a public machine: Download
- Quick tour of Python
- Editing window, variable explorer, and console
- Main numerical types: whole numbers (int) and numbers with decimals (float)
- + - * // (rounded division) and % (remainder / modula) produce in if both sides are an int, float if either or both are floats
- / (regular division) and // (rounded division) produces float with ints or floats
- ** to do powers
- Python doesn't know everything to start with; may need to import things
import MODULEmeans usingMODULE.function()to runimport MODULE as NAMEmeans usingNAME.function()to run
VAR = input("prompt: ")will ask the user for a value and stores whatever they type as a stringNUM = int(VAR)will convert the item in VAR to an integer if it looks like an integer; error otherwise
Lecture 3 - "Number" Types
- Finished prime number checker - code is available in the Box drive for the class under Lectures / Lec03
- Looked at for loops for running code multiple times
- Looked at if...else trees for making decisions
- Created a variable to track whether we thought the number was prime
- Python is a "typed" language - variables have types. We will use several types:
- Focus of the day: int, float, and array
- Focus a little later: string, list, tuple
- Focus later: dictionary, set
- Focus way later: map, filter, zip
- int: integers; Python 3 can store these perfectly
- float: floating point numbers - "numbers with decimal points" - Python sometimes has problems storing floating point items exactly
- array
- Requires numpy, usually with
import numpy as np - Organizational unit for storing rectangular arrays of numbers
- Generally create with np.array(LIST) where depth of nested LIST is dimensionality of array
- np.array([1, 2, 3]) is a 1-dimensional array with 3 elements
- np.array([[1, 2, 3], [4, 5, 6]]) is a 2-dimension array with 2 rows and 3 columns
- Requires numpy, usually with
- Math with "Number" types works the way you expect
- ** * / // % + -
- With arrays, * and / work element by element; *matrix* multiplication is a different character (specifically, @)
- Relational operators can compare "Number" Types and work the way you expect with True or False as an answer
- < <= == >= > !=
- With arrays, either same size or one is a single value; result will be an array of True and False the same size as the array
- Slices allow us to extract information from a collection or change information in mutable collections
- a[0] is the element in a at the start
- a[3] is the element in a three away from the start
- a[-1] is the last element of a
- a[-2] is the second-to-last element of a
- a[:] is all the elements in a because what is really happening is:
- a[start:until] where start is the first index and until is just *past* the last index;
- a[3:7] will return a[3] through a[6] in a 4-element array
- a[start:until:increment] will skip indices by increment instead of 1
- To go backwards, a[start:until:-increment] will start at an index and then go backwards until getting at or just past until.
- For 2-D arrays, you can index items with either separate row and column indices or indices separated by commas:
- a[2][3] is the same as a[2, 3]
- Only works for arrays!
Lecture 4 - Other Types
- Lists are set off with [ ] and entries can be any valid type (including other lists!); entries can be of different types from other entries; list items can be changed and mutable items within lists can be changed. Lists can be "grown" by using += with the list.
- Tuples are indicated by commas without square brackets (and are usually shown with parentheses - which are required if trying to make a tuple an entry in a tuple or a list); tuple items cannot be changed but mutable items within tuples can be
- Strings are set off with " " or ' ' and contain characters; string items cannot be changed
- For lists, tuples, and strings:
- Using + concatenates the two collections
- Using * with them makes creates a collection with the orignal repeated that many times
- Using += will create a new item with something appended to the old item; the "something" needs to be the same type (list, tuple, or string); this may seem to break the "can't be changed" rule but really
a += bisa = a + bwhich creates a newa.
- Characters in strings have "numerical" values based on the ASCII table (https://www.asciitable.com/)
- Numbers are earlier than lower case letters; lower case letters are earlier than upper case letters
- Strings are sorted character by character; if one string is shorter than another, it is considered less
- " Hello" < "Hi" since the "e" comes before the "i"
- "Zebra" < "apple" since the upper case "Z" is before the lower case "a"
- "go" < "gone" since the first two characters match and then the word is done
- To get the numerical value of a single character, use
ord("A")or replace the A with the character you want - To get the character a number represents, use
chr(NUM) - To apply either ord or chr to multiple items, use a
map; to see the results, make alistout of the map - Trinket
- To read more:
Lecture 5 - Format and Functions
- Creating formatted strings using {} and .format() (format strings, standard format specifiers) -- focus was on using s for string and e or f for numerical types, minimumwidth.precision, and possibly a + in front to force printing + for positive numbers.
- Using {} by themselves will substitute items in order from the
format()function into the string that gets created - Putting a number in the {} will tell
formatwhich thing to get - Format specification comes after a : in the {}; if you do not specify a location index, you still have to put a colon in the {}
- {:s} means string and {:Xs} where X is an integer means reserve at least that much space for a left-formatted string
- {:f} means floating point (default 6 digits after decimal point) and {:X.Yf} reserves at least X spaces (including + or - and the . if it is there) with Y digits after the decimal point for t right-justified number
- {:e} means floating point (default 6 digits after decimal point) and {:X.Ye} reserves at least X spaces (including + or - and the . if it is there and the letter e and the + or - after the e and the two or three digit number after that) with Y digits after the decimal point for t right-justified number
- Using {} by themselves will substitute items in order from the
- Aside - Format Specification Mini-Language has all the possibilities; we will cover some but not all of these in later classes
- You can enter numbers in scientific notation with a number followed by the letter 3 and then a number or negative number for the power of 10; for example,
x = 6.02e23ore = -1.6e-19- float can convert scientific notation as well:
float("1e-5")
- Defined functions can be multiple lines of code and have multiple outputs.
def FNAME(local1, local2, ...): CODE return THING1, THING2, ...
- Four different types of input parameters - we only really talked about the first kind:
- Required (listed first)
- We will cover the other kinds later
- Named with defaults (second)
- Additional positional arguments ("*args") (third)
- Function will create a tuple containing these items in order
- Additional keyword arguments ("**kwargs") (last)
- Function will create a dictionary of keyword and value pairs
- Function ends when indentation stops or when the function hits a return statement
- Return returns single item as an item of that type; if there are multiple items returned, they are stored and returned in a tuple
- If there is a left side to the function call, it either needs to be a single variable name or a tuple with as many entries as the number of items returned
- Four different types of input parameters - we only really talked about the first kind:
Lecture 6 - Relational Operators, Decisions, and Loops
- <= < == >= > != work with many types; just be careful about interpreting
notcan reverse whileandandorcan combine logical expressions- Basics of decisions using if...elif...else
- Must have logic after if
- Can have as many elif with logic after
- Can have an else without logic at the end
- Flow is solely dependent on indentation!
- Branches can contain other trees for follow-up questions
- Movie ratings.
- Basics of while loops and for loops.
- The Price Is Right game!
Lecture 7 - More Loops and Logical Masks
- Using a list to keep track of counts
- Using the
enumeratetype to provide a collection of indices and values to a loop - Basics of Python:Logical Masks
Lecture 8 - Dictionaries
- Dictionaries are collections of key : value pairs set off with { }; keys can be any immutable type (int, float, string, tuple) and must be unique; values can be any type and do not need to be unique
- Dictionary at tutorialspoint
- Storing values in a dictionary
- Bar chart demo
- Translation demo with Morse code and NATO phonetic alphabet
Lecture 9 - Iterative Methods
- Taylor series fundamentals
- Maclaurin series approximation for exponential uses Chapra 4.2 to compute terms in an infinite sum.
- so
- Newton Method for finding square roots uses Chapra 4.2 to iteratively solve using a mathematical map. To find \(y\) where \(y=\sqrt{x}\):
\( \begin{align} y_{init}&=1\\ y_{new}&=\frac{y_{old}+\frac{x}{y_{old}}}{2} \end{align} \) - See Python version of Fig. 4.2 and modified version of 4.2 in the Resources section of Sakai page under Chapra Pythonified
Lecture 10 - Binary
- Different number systems convey information in different ways.
- Roman Numerals
- Chinese Numbers
- Binary Numbers
- We went through how to convert between decimal and binary
- Floats (specifically double precision floats) are stored with a sign bit, 52 fractional bits, and 11 exponent bits. The exponent bits form a code:
- 0 (or 00000000000): the number is either 0 or a denormal
- 2047 (or 11111111111): the number is either infinite or not-a-number
- Others: the power of 2 for scientific notation is 2**(code-1023)
- The largest number is thus just *under* 2**1024 (ends up being (2-2**-52)**1024\(\approx 1.798\times 10^{308}\).
- The smallest normal number (full precision) is 2**(-1022)\(\approx 2.225\times 10^{-308}\).
- The smallest denormal number (only one significant binary digit) is 2**(-1022)/2**53 or 5e-324.
- When adding or subtracting, Python can only operate on the common significant digits - meaning the smaller number will lose precision.
- (1+1e-16)-1=0 and (1+1e-15)-1=1.1102230246251565e-15
- Avoid intermediate calculations that cause problems: if x=1.7e308,
- (x+x)/x is inf
- x/x + x/x is 2.0
- $$e^x=\lim_{n\rightarrow \infty}\left(1+\frac{x}{n}\right)^n$$
# Exponential Demo
<syntaxhighlightlang=python> import numpy as np import matplotlib.pyplot as plt
def exp_calc(x, n):
return (1 + x/n)**n
if __name__ == "__main__":
n = np.logspace(0, 17, 1000)
y = exp_calc(1, n)
fig, ax = plt.subplots(num=1, clear=True)
ax.semilogx(n, y)
fig.savefig('ExpDemoPlot1.png')
# Focus on right part
n = np.logspace(13, 16, 1000)
y = exp_calc(1, n)
fig, ax = plt.subplots(num=2, clear=True)
ax.semilogx(n, y)
fig.savefig('ExpDemoPlot2.png')
</syntaxhighlight>
- Want to see Amharic?
list(map(chr, range(4608, 4992)))
- Want to see the Greek alphabet?
for k in range(913,913+25):
print(chr(k), chr(k+32))
Lecture 11 - Monte Carlo Methods
- From Wikipedia: Monte Carlo method
- Walker demo