Difference between revisions of "Complex Numbers"
| (19 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| + | == Introduction == | ||
In the field of Mathematics, people had to come up with some | In the field of Mathematics, people had to come up with some | ||
satisfactory way to deal with the problems that arose when one tried | satisfactory way to deal with the problems that arose when one tried | ||
| Line 6: | Line 7: | ||
blossomed as engineers and physicists saw applications for what the | blossomed as engineers and physicists saw applications for what the | ||
theorists had developed. The idea is that a number ''n'' | theorists had developed. The idea is that a number ''n'' | ||
| − | can be made up of two parts: a real part | + | can be made up of two parts: a real part <math>\Re\{\mathbf{n}\}</math> and an |
| − | imaginary part | + | imaginary part <math>\Im\{\mathbf{n}\}</math>. |
These parts can be plotted - much like ''x'' and ''y'' coordinates - in | These parts can be plotted - much like ''x'' and ''y'' coordinates - in | ||
what is called the ''complex plane''. | what is called the ''complex plane''. | ||
| Line 18: | Line 19: | ||
\mathbf{n} = \Re\{\mathbf{n}\} + j\Im\{\mathbf{n}\}=n_r + jn_i | \mathbf{n} = \Re\{\mathbf{n}\} + j\Im\{\mathbf{n}\}=n_r + jn_i | ||
</math> | </math> | ||
| − | </center> | + | </center> |
where ''j'' is <math>\sqrt{-1}</math>. This gives all the information you need to | where ''j'' is <math>\sqrt{-1}</math>. This gives all the information you need to | ||
figure out the number. Now imagine that this is a point plotted | figure out the number. Now imagine that this is a point plotted | ||
| Line 27: | Line 28: | ||
<center> | <center> | ||
<math> | <math> | ||
| − | \mbox{magnitude}(\mathbf{n})=|\mathbf{n}|=n=\sqrt{\left(\Re\{n\}\right)^2 | + | \mbox{magnitude}(\mathbf{n})=|\mathbf{n}|=n=\sqrt{\left(\Re\{\mathbf{n}\}\right)^2 |
| − | +\left(\Im\{n\}\right)^2}=\sqrt{n_r^2+n_i^2} | + | +\left(\Im\{\mathbf{n}\}\right)^2}=\sqrt{n_r^2+n_i^2} |
</math> | </math> | ||
<math> | <math> | ||
\mbox{direction}(\mathbf{n})=\angle\mathbf{n}=\theta_n= | \mbox{direction}(\mathbf{n})=\angle\mathbf{n}=\theta_n= | ||
| − | \arctan(\Im\{n\}, \Re\{n\})=\arctan(n_i, n_r) | + | \arctan(\Im\{\mathbf{n}\}, \Re\{\mathbf{n}\})=\arctan(n_i, n_r) |
</math> | </math> | ||
</center> | </center> | ||
| Line 58: | Line 59: | ||
<center> | <center> | ||
<math> | <math> | ||
| − | \Re\{\mathbf{n}\} | + | \Re\{\mathbf{n}\}=n_r=n\cos\left(\theta_n\right) ~~~~~~~~~~~ |
| − | \Im\{\mathbf{n}\} | + | \Im\{\mathbf{n}\}=n_i=n\sin\left(\theta_n\right) |
</math> | </math> | ||
</center> | </center> | ||
| − | and | + | and '''n''' can be written as: |
| − | \ | + | <center><math> |
| − | { | + | \mathbf{n}=n\cos\left(\theta_n\right)+jn\sin\left(\theta_n\right)= |
n\left(\cos\left(\theta_n\right)+j\sin\left(\theta_n\right)\right) | n\left(\cos\left(\theta_n\right)+j\sin\left(\theta_n\right)\right) | ||
| − | + | </math></center> | |
| − | |||
| − | + | ==Euler Notation== | |
In representing complex numbers, you should note the following | In representing complex numbers, you should note the following | ||
| − | Maclaurin Series for | + | Maclaurin Series for <math>\cos(\theta)</math> and <math>\sin(\theta)</math>: |
| − | \begin{align | + | <center><math> |
| + | \begin{align} | ||
\cos(\theta)= | \cos(\theta)= | ||
\frac{\theta^0}{0!}-\frac{\theta^2}{2!}+\frac{\theta^4}{4!}-...&= | \frac{\theta^0}{0!}-\frac{\theta^2}{2!}+\frac{\theta^4}{4!}-...&= | ||
| Line 79: | Line 80: | ||
\frac{\theta^1}{1!}-\frac{\theta^3}{3!}+\frac{\theta^5}{5!}-...&= | \frac{\theta^1}{1!}-\frac{\theta^3}{3!}+\frac{\theta^5}{5!}-...&= | ||
\sum_{n=0,~n\mbox{ odd}}^{\infty}\frac{(-1)^{(n-1)/2}\theta^n}{n!} | \sum_{n=0,~n\mbox{ odd}}^{\infty}\frac{(-1)^{(n-1)/2}\theta^n}{n!} | ||
| − | \end{align | + | \end{align} |
| − | Now for some algebraic manipulation. First, note that the | + | </math></center> |
| − | in the | + | Now for some algebraic manipulation. First, note that the <math>(-1)^{n/2}</math> term |
| − | + | in the <math>\cos</math> series can be rewritten using the fact that | |
| − | \begin{align | + | <math>(-1)^{1/2}=j</math>: |
| + | <center><math> | ||
| + | \begin{align} | ||
(-1)^{n/2} = ((-1)^{1/2})^n = (j)^n | (-1)^{n/2} = ((-1)^{1/2})^n = (j)^n | ||
| − | \end{align | + | \end{align} |
| − | Next, in the | + | </math></center> |
| − | + | Next, in the <math>\sin</math> series, the | |
| − | \begin{align | + | <math>(-1)^{(n-1)/2}</math> term can be split up, noting that: |
| + | <center><math> | ||
| + | \begin{align} | ||
(-1)^{(n-1)/2}&=(-1)^{-1/2}(-1)^{n/2} | (-1)^{(n-1)/2}&=(-1)^{-1/2}(-1)^{n/2} | ||
| − | \end{align | + | \end{align} |
| + | </math></center> | ||
and from above, rewritten as | and from above, rewritten as | ||
| − | \begin{align | + | <center><math> |
| + | \begin{align} | ||
(-1)^{-1/2}(-1)^{n/2}&= | (-1)^{-1/2}(-1)^{n/2}&= | ||
(-1)(-1)^{1/2}(-1)^{n/2}= | (-1)(-1)^{1/2}(-1)^{n/2}= | ||
-j~(j)^n | -j~(j)^n | ||
| − | \end{align | + | \end{align} |
| + | </math></center> | ||
which means the two Maclaurin Series can be written as: | which means the two Maclaurin Series can be written as: | ||
| − | \begin{align | + | <center><math> |
| + | \begin{align} | ||
\cos(\theta)&= | \cos(\theta)&= | ||
\sum_{n=0,~n\mbox{ even}}^{\infty}\frac{(j\theta)^n}{n!}\\ | \sum_{n=0,~n\mbox{ even}}^{\infty}\frac{(j\theta)^n}{n!}\\ | ||
\sin(\theta)&= | \sin(\theta)&= | ||
-j\sum_{n=0,~n\mbox{ odd}}^{\infty}\frac{(j\theta)^n}{n!} | -j\sum_{n=0,~n\mbox{ odd}}^{\infty}\frac{(j\theta)^n}{n!} | ||
| − | \end{align | + | \end{align} |
| − | In the latter case, multiplying both sides by | + | </math></center> |
| − | + | In the latter case, multiplying both sides by <math>j</math> and recognizing that | |
| − | \begin{align | + | <math>-j^2=1</math>, we obtain: |
| + | <center><math> | ||
| + | \begin{align} | ||
j\sin(\theta)&= | j\sin(\theta)&= | ||
\sum_{n=0,~n\mbox{ odd}}^{\infty}\frac{(j\theta)^n}{n!} | \sum_{n=0,~n\mbox{ odd}}^{\infty}\frac{(j\theta)^n}{n!} | ||
| − | \end{align | + | \end{align} |
| − | What Euler noticed was the following - one representation of | + | </math></center> |
| + | What Euler noticed was the following - one representation of <math>e^x</math> is | ||
a Maclaurin series of: | a Maclaurin series of: | ||
| − | \begin{align | + | <center><math> |
| + | \begin{align} | ||
e^x=\frac{x^0}{0!} + \frac{x^1}{1!} + \frac{x^2}{2!} + ... &= | e^x=\frac{x^0}{0!} + \frac{x^1}{1!} + \frac{x^2}{2!} + ... &= | ||
\sum_{n=0}^{\infty}\frac{x^n}{n!} | \sum_{n=0}^{\infty}\frac{x^n}{n!} | ||
| − | \end{align | + | \end{align} |
| − | Simply substituting | + | </math></center> |
| − | \begin{align | + | Simply substituting <math>x=j\theta</math> yields |
| + | <center><math> | ||
| + | \begin{align} | ||
e^{j\theta}=\frac{(j\theta)^0}{0!} + \frac{(j\theta)^1}{1!} + \frac{(j\theta)^2}{2!} + ... &= | e^{j\theta}=\frac{(j\theta)^0}{0!} + \frac{(j\theta)^1}{1!} + \frac{(j\theta)^2}{2!} + ... &= | ||
\sum_{n=0}^{\infty}\frac{(j\theta)^n}{n!} | \sum_{n=0}^{\infty}\frac{(j\theta)^n}{n!} | ||
| − | \end{align | + | \end{align} |
| − | which is the sum of the Maclaurin Series for | + | </math></center> |
| − | + | which is the sum of the Maclaurin Series for <math>\cos(\theta)</math> and | |
| − | \begin{align | + | <math>j\sin(\theta)</math>. In other words, |
| + | <center><math> | ||
| + | \begin{align} | ||
e^{j\theta} = \cos(\theta) + j\sin(\theta) | e^{j\theta} = \cos(\theta) + j\sin(\theta) | ||
| − | \end{align | + | \end{align} |
| + | </math></center> | ||
Using this, you can write a complex number as: | Using this, you can write a complex number as: | ||
| − | \begin{align | + | <center><math> |
| − | { | + | \begin{align} |
| − | \end{align | + | \mathbf{n}&=n(\cos(\theta)+j\sin(\theta))=ne^{j\theta_n} |
| − | This gives rise to one of | + | \end{align} |
| − | least according to | + | </math></center> |
| − | + | This gives rise to one of "The Greatest Equations Ever" (at | |
| − | \begin{align | + | least according to '''physicsweb'''<ref name="PhysicsWeb">[http://physicsweb.org/articles/world/17/10/2 Physics Web], accessed October 12, 2006</ref>): |
| + | <center><math> | ||
| + | \begin{align} | ||
e^{j\pi}+1&=0 | e^{j\pi}+1&=0 | ||
| − | \end{align | + | \end{align} |
| − | which combines an infinite sum ( | + | </math></center> |
| − | irrational ratio (the ever mysterious | + | which combines an infinite sum (<math>e</math>), the imaginary number (<math>j</math>), an |
| + | irrational ratio (the ever mysterious <math>\pi</math>), and unity (1) and, | ||
through an equality (=), relates them all to...nothing (0). | through an equality (=), relates them all to...nothing (0). | ||
| − | |||
| − | + | ==Addition and Subtraction== | |
| − | |||
Addition and subtraction are performed component-wise and are done most | Addition and subtraction are performed component-wise and are done most | ||
easily by using the rectangular representation. Assume you have two | easily by using the rectangular representation. Assume you have two | ||
complex numbers: | complex numbers: | ||
| − | \begin{align | + | <center><math> |
| − | {\ | + | \begin{align} |
| + | {\mathbf n}=a+jb&=ne^{j\theta_n} | ||
& | & | ||
| − | {\ | + | {\mathbf m}=c+jd&=me^{j\theta_m} |
| − | \end{align | + | \end{align} |
| + | </math></center> | ||
and you want to add or subtract them. Adding or subtracting the | and you want to add or subtract them. Adding or subtracting the | ||
components and then collecting the real parts and the imaginary parts gives: | components and then collecting the real parts and the imaginary parts gives: | ||
| − | \begin{align | + | <center><math> |
| − | {\ | + | \begin{align} |
| − | {\ | + | {\mathbf n} + {\mathbf m} &= (a+c) + j(b+d)& |
| − | \end{align | + | {\mathbf n} - {\mathbf m} &= (a-c) + j(b-d) |
| + | \end{align} | ||
| + | </math></center> | ||
| − | + | ==Multiplication and Division== | |
| − | |||
Multiplication and division are a little more difficult. The best | Multiplication and division are a little more difficult. The best | ||
notation to use is the Euler one. To multiply the two | notation to use is the Euler one. To multiply the two | ||
numbers given in the section above: | numbers given in the section above: | ||
| − | \begin{align | + | <center><math> |
| − | {\ | + | \begin{align} |
| − | {\ | + | {\mathbf o}&={\mathbf n} {\mathbf m}=ne^{j\theta_n}~me^{j\theta_m}\\ |
| + | {\mathbf o}&=nme^{j(\theta_n+\theta_m)}= | ||
oe^{j\theta_o} | oe^{j\theta_o} | ||
| − | \end{align | + | \end{align}</math></center> |
You can then get the rectangular representation of this by converting | You can then get the rectangular representation of this by converting | ||
from the Euler representation writing: | from the Euler representation writing: | ||
| − | \begin{align | + | <center><math> |
| − | {\ | + | \begin{align} |
| + | {\mathbf | ||
o}&=nm\cos\left(\theta_n+\theta_m\right)+jnm\sin\left(\theta_n+\theta_m\right) | o}&=nm\cos\left(\theta_n+\theta_m\right)+jnm\sin\left(\theta_n+\theta_m\right) | ||
| − | \end{align | + | \end{align}</math></center> |
Another way to do multiplication is by using the rectangular | Another way to do multiplication is by using the rectangular | ||
representation and FOILing: | representation and FOILing: | ||
| − | \begin{align | + | <center><math> |
| − | {\ | + | \begin{align} |
| − | {\ | + | {\mathbf o}&={\mathbf n} {\mathbf m}=(a+jb)(c+jd)\\ |
| − | {\ | + | {\mathbf o}&=ac+jad+jbc+j^2bd\\ |
| − | \end{align | + | {\mathbf o}&=(ac-bd)+j(ad+bc)=\Re\{ {\mathbf o\} }+j\Im \{ {\mathbf o\} } |
| + | \end{align}</math></center> | ||
Division is easiest using the Euler representation: | Division is easiest using the Euler representation: | ||
| − | \begin{align | + | <center><math> |
| − | {\ | + | \begin{align} |
| + | {\mathbf p}&=\frac{ {\mathbf n} }{ {\mathbf m} }= | ||
\frac{ne^{j\theta_n}}{me^{j\theta_m}}\\ | \frac{ne^{j\theta_n}}{me^{j\theta_m}}\\ | ||
| − | {\ | + | {\mathbf p}&= |
\frac{n}{m}e^{j(\theta_n-\theta_m)}=pe^{j\theta_p} | \frac{n}{m}e^{j(\theta_n-\theta_m)}=pe^{j\theta_p} | ||
| − | \end{align | + | \end{align}</math></center> |
Division using the rectangular representation is a little more difficult. | Division using the rectangular representation is a little more difficult. | ||
| − | You have to use the | + | You have to use the ''complex conjugate'' of the denominator to get |
| − | rid of any | + | rid of any <math>j</math>'s on the bottom. The complex conjugate of a number is |
the number with the sign on its imaginary part switched. It is also the | the number with the sign on its imaginary part switched. It is also the | ||
number with the sign on its angle switched. The complex conjugate is | number with the sign on its angle switched. The complex conjugate is | ||
| − | represented by a superscript | + | represented by a superscript *. For example, <math>{\mathbf n}^*</math> is: |
| − | \begin{align | + | <center><math> |
| − | {\ | + | \begin{align} |
| − | \end{align | + | {\mathbf n}^*=a-jb&=n\angle-\theta_n=ne^{-j\theta_n} |
| + | \end{align}</math></center> | ||
Note that a number multiplied by its own complex conjugate will give | Note that a number multiplied by its own complex conjugate will give | ||
the magnitude of that number squared. The following shows this using | the magnitude of that number squared. The following shows this using | ||
all three notations: | all three notations: | ||
| − | \begin{align | + | <center><math> |
| − | {\ | + | \begin{align} |
| − | {\ | + | {\mathbf n}{\mathbf n}^*&=(a+jb)(a-jb)=a^2+b^2=n^2\\ |
| − | {\ | + | {\mathbf n}{\mathbf n}^*&=(n\angle\theta_n)(n\angle-\theta_n)=n^2\angle 0=n^2\\ |
| + | {\mathbf n}{\mathbf n}^*&= | ||
\left(ne^{j\theta_n}\right)\left(ne^{-j\theta_n}\right)= | \left(ne^{j\theta_n}\right)\left(ne^{-j\theta_n}\right)= | ||
n^2e^{j0}=n^2 | n^2e^{j0}=n^2 | ||
| − | \end{align | + | \end{align}</math></center> |
Division thus proceeds as follows: | Division thus proceeds as follows: | ||
| − | \begin{align | + | <center><math> |
| − | {\ | + | \begin{align} |
| − | \frac{{\ | + | {\mathbf p}=\frac{ {\mathbf n} }{ {\mathbf m} }= |
| − | \frac{a+jb}{c+jd}\frac{c-jd}{c-jd} = | + | \frac{ {\mathbf n} }{ {\mathbf m} } \frac{ {\mathbf m}^* }{ {\mathbf m}^* }&= |
| − | \frac{(ac+bd)+j(-ad+bc)}{c^2+d^2}= | + | \frac{a+jb}{c+jd}\frac{c-jd}{c-jd}\\ |
| − | \frac{ac+bd}{c^2+d^2}+j\frac{-ad+bc}{c^2+d^2}= | + | &= \frac{(ac+bd)+j(-ad+bc)}{c^2+d^2}\\ |
| − | \Re\ | + | &=\frac{ac+bd}{c^2+d^2}+j\frac{-ad+bc}{c^2+d^2}\\ |
| − | \end{align | + | &=\Re\left\{ {\mathbf p}\right\}+j\Im\left\{ {\mathbf p}\right\} |
| + | \end{align}</math></center> | ||
| − | + | ==Elongation / Contraction== | |
| − | |||
Sometimes, you will only need to change the magnitude of a complex | Sometimes, you will only need to change the magnitude of a complex | ||
| − | number. This is the same as only changing the | + | number. This is the same as only changing the ''length'' and not |
| − | the | + | the ''direction'' of a vector. Multiplication by a ''scalar'' |
| − | only changes the magnitude. A | + | only changes the magnitude. A ''scalar'' is not a complex number |
because it does not have an angle associated with it. The complex | because it does not have an angle associated with it. The complex | ||
equivalent of a scalar is a number having an angle of 0 radians. | equivalent of a scalar is a number having an angle of 0 radians. | ||
| − | Multiplication by a scalar is simple. Assume that | + | Multiplication by a scalar is simple. Assume that <math>s</math> is a scalar, |
| − | \begin{align | + | <center><math> |
| − | {\ | + | \begin{align} |
| + | {\mathbf t}=s{\mathbf n}=sa+jsb=sn\angle\theta_n= | ||
sne^{j\theta_n} | sne^{j\theta_n} | ||
| − | \end{align | + | \end{align}</math></center> |
| − | + | ==Rotation== | |
| − | |||
You may also simply want to rotate a complex number around the | You may also simply want to rotate a complex number around the | ||
| − | origin. For example, once you find the first | + | origin. For example, once you find the first <math>r</math>th root of a number |
| − | you really only need to rotate it around | + | you really only need to rotate it around <math>\frac{2\pi}{r}\,\!</math> to get the |
next root. This is done by multiplying by a complex number of unit | next root. This is done by multiplying by a complex number of unit | ||
| − | magnitude with some angle. Assume you want to rotate {\ | + | magnitude with some angle. Assume you want to rotate <math>{\mathbf n}</math> |
| − | by an angle | + | by an angle <math>\theta_i</math> radians counterclockwise around the origin: |
| − | \begin{align | + | <center><math> |
| − | {\ | + | \begin{align} |
| + | {\mathbf u}=\left(1\angle\theta_i\right) | ||
\left(n\angle\theta_n\right)= | \left(n\angle\theta_n\right)= | ||
| − | ne^{j\theta_i}e^{j\theta_n}=ne^{\left( | + | ne^{j\theta_i}e^{j\theta_n}=ne^{j\left(\theta_i+\theta_n\right)}= |
ue^{j\theta_u} | ue^{j\theta_u} | ||
| − | \end{align | + | \end{align}</math></center> |
You can also multiply by the rectangular representation of the angle | You can also multiply by the rectangular representation of the angle | ||
| − | \begin{align | + | <center><math> |
| + | \begin{align} | ||
e^{j\theta_i}&=\cos\left(\theta_i\right)+j\sin\left(\theta_i\right)\\ | e^{j\theta_i}&=\cos\left(\theta_i\right)+j\sin\left(\theta_i\right)\\ | ||
| − | {\ | + | {\mathbf u}&=\left(\cos\left(\theta_i\right)+j\sin\left(\theta_i\right)\right) |
\left(a+jb\right)\\ | \left(a+jb\right)\\ | ||
| − | + | &=\left(a\cos\left(\theta_i\right)-b\sin\left(\theta_i\right)\right) | |
| − | + | +j\left(b\cos\left(\theta_i\right)+a\sin\left(\theta_i\right)\right)\\ | |
| − | +j\left(b\cos\left(\theta_i\right)+a\sin\left(\theta_i\right)\right)= | + | &=\Re\{ {\mathbf u\} }+j\Im\{ {\mathbf u\} } |
| − | \Re\ | + | \end{align}</math></center> |
| − | \end{align | ||
From this, you should recognize that multiplication by | From this, you should recognize that multiplication by | ||
| − | + | <math>j</math>, which is also <math>1\angle90^{\circ}</math>, is the same as a | |
| − | counterclockwise rotation of | + | counterclockwise rotation of <math>90^{\circ}</math> |
| − | + | ==Integer Powers== | |
| − | |||
Integer powers of complex numbers are best taken using Euler notation: | Integer powers of complex numbers are best taken using Euler notation: | ||
| − | \begin{align | + | <center><math> |
| − | {\ | + | \begin{align} |
| − | \end{align | + | {\mathbf v}&={\mathbf n}^p=\left(ne^{j\theta_n}\right)^p=n^pe^{jp\theta_n} |
| − | This represents both a change in length (from | + | \end{align}</math></center> |
| − | change in direction (from | + | This represents both a change in length (from <math>n</math> to <math>n^{p}</math>) and a |
| + | change in direction (from <math>\theta_n</math> to <math>p\theta_n</math>). | ||
| − | + | ===Integer Roots=== | |
Roots of complex numbers are also best taken using Euler | Roots of complex numbers are also best taken using Euler | ||
| − | notation. To take the | + | notation. To take the <math>r</math>th root of a number: |
| − | \begin{align | + | <center><math> |
| − | {\ | + | \begin{align} |
| + | {\mathbf n}^{\frac{1}{r}}=\left(ne^{j\theta_n}\right)^{\frac{1}{r}}= | ||
n^{\frac{1}{r}}e^{j\frac{\theta_n}{r}} | n^{\frac{1}{r}}e^{j\frac{\theta_n}{r}} | ||
| − | \end{align | + | \end{align}</math></center> |
| − | In other words, the | + | In other words, the ''magnitude'' of the root is equal to the root |
| − | of the original magnitude, and the | + | of the original magnitude, and the ''direction'' of the root is |
equal to the direction of the original number divided by whatever root | equal to the direction of the original number divided by whatever root | ||
| − | you are taking. This is the | + | you are taking. This is the ''primary'' root. |
Note that using the Euler notation, any number can be | Note that using the Euler notation, any number can be | ||
represented in an infinite number of ways simply by adding multiples of | represented in an infinite number of ways simply by adding multiples of | ||
| − | + | <math>2\pi</math> to the angle. This is the same as going around a complete | |
circle and ending up where you started. In the above root: | circle and ending up where you started. In the above root: | ||
| − | \begin{align | + | <center><math> |
| − | {\ | + | \begin{align} |
| + | {\mathbf n}^{\frac{1}{r}}=\left(ne^{j\theta_n+j2\pi}\right)^{\frac{1}{r}} | ||
=n^{\frac{1}{r}}e^{\frac{j\theta_n}{r}+j\frac{2\pi}{r}} | =n^{\frac{1}{r}}e^{\frac{j\theta_n}{r}+j\frac{2\pi}{r}} | ||
| − | \end{align | + | \end{align}</math></center> |
This gives another, equally valid root of the number. In fact, any | This gives another, equally valid root of the number. In fact, any | ||
| − | number other than {\ | + | number other than {\mathbf 0} has <math>r</math> <math>r</math>th roots. These roots will be |
| − | evenly divided across the full range of | + | evenly divided across the full range of <math>2\pi</math>. They will all |
have the same magnitude. You can draw a circle with a radius of the | have the same magnitude. You can draw a circle with a radius of the | ||
| − | + | <math>r</math>th root of <math>n</math> and it will pass through all <math>r</math> roots of {\mathbf n}. | |
| − | + | ===Example 1=== | |
| − | Find all the cube roots of | + | Find all the cube roots of <math>1+j0</math>. Since the magnitude of this number |
is 1 and the direction is 0, the first cube root has a magnitude of | is 1 and the direction is 0, the first cube root has a magnitude of | ||
| − | + | <math>1^{\frac{1}{3}}=1</math> and a direction of <math>0/3=0</math>. Since the roots are | |
| − | equally spaced, they will be | + | equally spaced, they will be <math>\frac{2\pi}{3}\,\!</math> apart, meaning: |
| − | \begin{align | + | <center><math> |
| + | \begin{align} | ||
\left(1+j0\right)^{\frac{1}{3}} &=1e^{j0}=\cos 0 + j\sin 0 = 1\\ | \left(1+j0\right)^{\frac{1}{3}} &=1e^{j0}=\cos 0 + j\sin 0 = 1\\ | ||
\left(1+j0\right)^{\frac{1}{3}} &=1e^{j\frac{2}{3}\pi}= | \left(1+j0\right)^{\frac{1}{3}} &=1e^{j\frac{2}{3}\pi}= | ||
| Line 310: | Line 342: | ||
\left(1+j0\right)^{\frac{1}{3}} &=1e^{j\frac{4}{3}\pi}= | \left(1+j0\right)^{\frac{1}{3}} &=1e^{j\frac{4}{3}\pi}= | ||
\cos \frac{4}{3}\pi+j\sin \frac{4}{3}\pi= -0.5-j0.886 | \cos \frac{4}{3}\pi+j\sin \frac{4}{3}\pi= -0.5-j0.886 | ||
| − | \end{align | + | \end{align}</math></center> |
| − | + | ===Example 2=== | |
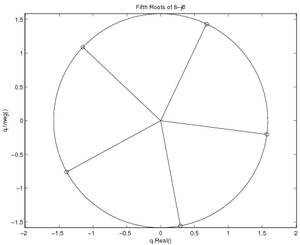
| − | + | [[File:FifthRoots.png|thumb|Fifth-roots]] | |
| − | Find all the fifth roots of | + | Find all the fifth roots of <math>{\mathbf n}=8-j6</math>. |
| + | |||
| + | First, find the magnitude | ||
and direction: | and direction: | ||
| − | \begin{align | + | <center><math> |
| + | \begin{align} | ||
n = \sqrt{8^2+6^2}&=10\\ | n = \sqrt{8^2+6^2}&=10\\ | ||
\theta_n=\arctan(-6,8)&=-0.64350~\mbox{rad} | \theta_n=\arctan(-6,8)&=-0.64350~\mbox{rad} | ||
| − | \end{align | + | \end{align}</math></center> |
| − | The magnitude and direction of the primary root | + | The magnitude and direction of the primary root <math>{\mathbf q_1}</math> |
will therefore be: | will therefore be: | ||
| − | \begin{align | + | <center><math> |
| + | \begin{align} | ||
q_1 = (10)^{\frac{1}{5}} &= 1.585 & | q_1 = (10)^{\frac{1}{5}} &= 1.585 & | ||
\theta_{q_1}&=\frac{-0.64350~\mbox{rad}}{5} = -0.1287~\mbox{rad} | \theta_{q_1}&=\frac{-0.64350~\mbox{rad}}{5} = -0.1287~\mbox{rad} | ||
| − | \end{align | + | \end{align}</math></center> |
In its rectangular representation, this is: | In its rectangular representation, this is: | ||
| − | \begin{align | + | <center><math> |
| − | {\ | + | \begin{align} |
| + | {\mathbf q_1} = 1.585\cos\left(-0.1287~\mbox{rad}\right)+ | ||
j1.585\sin\left(-0.1287~\mbox{rad}\right)= | j1.585\sin\left(-0.1287~\mbox{rad}\right)= | ||
1.572-j0.203 | 1.572-j0.203 | ||
| − | \end{align | + | \end{align}</math></center> |
The next four roots will be evenly spaced around the complex plane, so | The next four roots will be evenly spaced around the complex plane, so | ||
| − | they will be | + | they will be <math>\frac{2\pi}{5}\,\!</math> apart and have directions of: |
| − | \begin{align | + | <center><math> |
| + | \begin{align} | ||
\theta_{q_2}&=\theta_{q_1}+1*\frac{2\pi}{5}=1.128~\mbox{rad} & | \theta_{q_2}&=\theta_{q_1}+1*\frac{2\pi}{5}=1.128~\mbox{rad} & | ||
\theta_{q_3}&=\theta_{q_1}+2*\frac{2\pi}{5}=2.385~\mbox{rad}\\ | \theta_{q_3}&=\theta_{q_1}+2*\frac{2\pi}{5}=2.385~\mbox{rad}\\ | ||
\theta_{q_4}&=\theta_{q_1}+3*\frac{2\pi}{5}=3.641~\mbox{rad} & | \theta_{q_4}&=\theta_{q_1}+3*\frac{2\pi}{5}=3.641~\mbox{rad} & | ||
\theta_{q_5}&=\theta_{q_1}+4*\frac{2\pi}{5}=4.898~\mbox{rad} | \theta_{q_5}&=\theta_{q_1}+4*\frac{2\pi}{5}=4.898~\mbox{rad} | ||
| − | \end{align | + | \end{align}</math></center> |
By converting from Euler to rectangular notation, you can find: | By converting from Euler to rectangular notation, you can find: | ||
| − | \begin{align | + | <center><math> |
| − | {\ | + | \begin{align} |
| − | {\ | + | {\mathbf q_2}&=0.679+j1.432\\ |
| − | {\ | + | {\mathbf q_3}&=-1.152+j1.088\\ |
| − | {\ | + | {\mathbf q_4}&=-1.391-j0.759\\ |
| − | \end{align | + | {\mathbf q_5}&=0.292-j1.558 |
| − | These are shown in | + | \end{align}</math></center> |
| − | + | These are shown in the figure at right. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ==Non-integer Powers== | |
| − | |||
Non-integer powers and roots are more complicated. If you are only | Non-integer powers and roots are more complicated. If you are only | ||
| − | looking for the | + | looking for the ''primary'' power for any arbitrary scalar a |
then you can simply calculate: | then you can simply calculate: | ||
| − | \begin{align | + | <center><math>\begin{align} |
| − | {\ | + | {\mathbf q_p}=\left({\mathbf n}\right)^a=\left(ne^{j\theta_n}\right)^a |
=n^ae^{ja\theta_n} | =n^ae^{ja\theta_n} | ||
| − | \end{align | + | \end{align}</math></center> |
For rational powers (powers that can be represented by a fraction), | For rational powers (powers that can be represented by a fraction), | ||
you can first raise the complex number to the | you can first raise the complex number to the | ||
numerator and then take roots from the denominator. That is: | numerator and then take roots from the denominator. That is: | ||
| − | \begin{align | + | <center><math>\begin{align} |
| − | {\ | + | {\mathbf q_r}={\mathbf n}^{\left(\frac{t}{b}\right)}= |
\left(\left(ne^{j\theta_n}\right)^{t}\right)^{\frac{1}{b}}= | \left(\left(ne^{j\theta_n}\right)^{t}\right)^{\frac{1}{b}}= | ||
\left(n^{t}e^{jt\theta_n}\right)^{\frac{1}{b}} | \left(n^{t}e^{jt\theta_n}\right)^{\frac{1}{b}} | ||
| − | \end{align | + | \end{align}</math></center> |
| − | + | <!-- | |
| − | + | ==Calculator Functions== | |
| − | |||
The HP48 series of calculators - among others - has some helpful | The HP48 series of calculators - among others - has some helpful | ||
built-in functions for dealing with complex numbers. This tutorial is | built-in functions for dealing with complex numbers. This tutorial is | ||
| Line 405: | Line 436: | ||
the angle character (right (blue) shift on the {\tt SPC} button). The | the angle character (right (blue) shift on the {\tt SPC} button). The | ||
$\angle$ symbol will come up and you can enter your angle. See below | $\angle$ symbol will come up and you can enter your angle. See below | ||
| − | about radians versus degrees. Note that regardless of how you | + | about radians versus degrees. Note that regardless of how you ''enter'' |
your complex number, the HP will display it in the current display mode. | your complex number, the HP will display it in the current display mode. | ||
| Line 495: | Line 526: | ||
your complex number will change from polar to rectangular. Also, the | your complex number will change from polar to rectangular. Also, the | ||
{\tt R$\angle$Z} indicator will turn off. | {\tt R$\angle$Z} indicator will turn off. | ||
| − | |||
| − | + | --> | |
| − | + | ||
| + | ==Parting Thoughts== | ||
Decide early on a notation you like for complex numbers. Some | Decide early on a notation you like for complex numbers. Some | ||
possibilities are: | possibilities are: | ||
| − | \begin{align | + | <center><math>\begin{align} |
| − | {\ | + | {\mathbf N}~~~~~~~~\tilde{N}~~~~~~~~\mathbb{N} ~~~~~~~~\underline{N} |
| − | \end{align | + | \end{align}</math></center> |
| + | |||
For example, using complex variables to give Ohm's Law might look like: | For example, using complex variables to give Ohm's Law might look like: | ||
| − | \begin{align | + | <center><math>\begin{align} |
| − | \ | + | \mathbb{Z}&=\frac{\mathbb{V}}{\mathbb{I}} |
| − | \end{align | + | \end{align}</math></center> |
Make sure you know how your angles are represented (degrees or | Make sure you know how your angles are represented (degrees or | ||
| − | radians). If someone asks you | + | radians). If someone asks you "What is the cosine of 45," you need |
| − | to start getting the the habit of asking | + | to start getting the the habit of asking "radians or degrees?" even |
| − | though it may seem obvious. Also, if someone says | + | though it may seem obvious. Also, if someone says "the frequency is |
| − | ten, | + | ten," you need to always ask "in Hertz or radians per second?" |
Complex numbers are at the heart of many powerful tools in engineering. | Complex numbers are at the heart of many powerful tools in engineering. | ||
| Line 521: | Line 553: | ||
once you have practiced with them a little bit, and the time spent learning | once you have practiced with them a little bit, and the time spent learning | ||
about them will pay great dividends in the future. | about them will pay great dividends in the future. | ||
| + | {{Protected Class Document}} | ||
Latest revision as of 00:09, 21 November 2022
Contents
Introduction
In the field of Mathematics, people had to come up with some satisfactory way to deal with the problems that arose when one tried to take the square root of a negative number. Not happy with simply saying "there isn't one," the mathematicians came up with an object known as a complex number. The usefulness of this construct blossomed as engineers and physicists saw applications for what the theorists had developed. The idea is that a number n can be made up of two parts: a real part \(\Re\{\mathbf{n}\}\) and an imaginary part \(\Im\{\mathbf{n}\}\). These parts can be plotted - much like x and y coordinates - in what is called the complex plane.
There are many ways to represent a complex number. Of these, three stand out as being particularly useful. The first is the standard or rectangular representation:
\( \mathbf{n} = \Re\{\mathbf{n}\} + j\Im\{\mathbf{n}\}=n_r + jn_i \)
where j is \(\sqrt{-1}\). This gives all the information you need to figure out the number. Now imagine that this is a point plotted in 2D space where the real part is the x coordinate and the imaginary part is the y coordinate. You could figure out a magnitude and direction from the origin to this point and write the location in polar coordinates. The magnitude and direction would be given by:
\( \mbox{magnitude}(\mathbf{n})=|\mathbf{n}|=n=\sqrt{\left(\Re\{\mathbf{n}\}\right)^2 +\left(\Im\{\mathbf{n}\}\right)^2}=\sqrt{n_r^2+n_i^2} \) \( \mbox{direction}(\mathbf{n})=\angle\mathbf{n}=\theta_n= \arctan(\Im\{\mathbf{n}\}, \Re\{\mathbf{n}\})=\arctan(n_i, n_r) \)
where arctan with two arguments specifies that the answer will be
some angle between \(-\pi\) and \(\pi\) instead of the typical
limits of \(-\pi/2\) to \(\pi/2\). This distinction is important because
the two-argument version of arctan will give the proper angle between
the positive real axis and the complex number. Calculators usually
only have the one-argument version. In this case, you will use the
ratio \(n_i/n_r\) as your argument, but must make sure
your answer is in the proper quadrant.
Using the above, a complex number n can be represented:
\( \mathbf{n}=n\angle\theta_n \)
At this point, you should notice that n is the hypotenuse of a right triangle with an angle of \(\theta_n\) with respect to the horizontal. This means the real and imaginary parts can be written as:
\( \Re\{\mathbf{n}\}=n_r=n\cos\left(\theta_n\right) ~~~~~~~~~~~ \Im\{\mathbf{n}\}=n_i=n\sin\left(\theta_n\right) \)
and n can be written as:
Euler Notation
In representing complex numbers, you should note the following Maclaurin Series for \(\cos(\theta)\) and \(\sin(\theta)\):
Now for some algebraic manipulation. First, note that the \((-1)^{n/2}\) term in the \(\cos\) series can be rewritten using the fact that \((-1)^{1/2}=j\):
Next, in the \(\sin\) series, the \((-1)^{(n-1)/2}\) term can be split up, noting that:
and from above, rewritten as
which means the two Maclaurin Series can be written as:
In the latter case, multiplying both sides by \(j\) and recognizing that \(-j^2=1\), we obtain:
What Euler noticed was the following - one representation of \(e^x\) is a Maclaurin series of:
Simply substituting \(x=j\theta\) yields
which is the sum of the Maclaurin Series for \(\cos(\theta)\) and \(j\sin(\theta)\). In other words,
Using this, you can write a complex number as:
This gives rise to one of "The Greatest Equations Ever" (at least according to physicsweb[1]):
which combines an infinite sum (\(e\)), the imaginary number (\(j\)), an irrational ratio (the ever mysterious \(\pi\)), and unity (1) and, through an equality (=), relates them all to...nothing (0).
Addition and Subtraction
Addition and subtraction are performed component-wise and are done most easily by using the rectangular representation. Assume you have two complex numbers:
and you want to add or subtract them. Adding or subtracting the components and then collecting the real parts and the imaginary parts gives:
Multiplication and Division
Multiplication and division are a little more difficult. The best notation to use is the Euler one. To multiply the two numbers given in the section above:
You can then get the rectangular representation of this by converting from the Euler representation writing:
Another way to do multiplication is by using the rectangular representation and FOILing:
Division is easiest using the Euler representation:
Division using the rectangular representation is a little more difficult. You have to use the complex conjugate of the denominator to get rid of any \(j\)'s on the bottom. The complex conjugate of a number is the number with the sign on its imaginary part switched. It is also the number with the sign on its angle switched. The complex conjugate is represented by a superscript *. For example, \({\mathbf n}^*\) is:
Note that a number multiplied by its own complex conjugate will give the magnitude of that number squared. The following shows this using all three notations:
Division thus proceeds as follows:
Elongation / Contraction
Sometimes, you will only need to change the magnitude of a complex number. This is the same as only changing the length and not the direction of a vector. Multiplication by a scalar only changes the magnitude. A scalar is not a complex number because it does not have an angle associated with it. The complex equivalent of a scalar is a number having an angle of 0 radians. Multiplication by a scalar is simple. Assume that \(s\) is a scalar,
Rotation
You may also simply want to rotate a complex number around the origin. For example, once you find the first \(r\)th root of a number you really only need to rotate it around \(\frac{2\pi}{r}\,\!\) to get the next root. This is done by multiplying by a complex number of unit magnitude with some angle. Assume you want to rotate \({\mathbf n}\) by an angle \(\theta_i\) radians counterclockwise around the origin:
You can also multiply by the rectangular representation of the angle
From this, you should recognize that multiplication by \(j\), which is also \(1\angle90^{\circ}\), is the same as a counterclockwise rotation of \(90^{\circ}\)
Integer Powers
Integer powers of complex numbers are best taken using Euler notation:
This represents both a change in length (from \(n\) to \(n^{p}\)) and a change in direction (from \(\theta_n\) to \(p\theta_n\)).
Integer Roots
Roots of complex numbers are also best taken using Euler notation. To take the \(r\)th root of a number:
In other words, the magnitude of the root is equal to the root of the original magnitude, and the direction of the root is equal to the direction of the original number divided by whatever root you are taking. This is the primary root.
Note that using the Euler notation, any number can be represented in an infinite number of ways simply by adding multiples of \(2\pi\) to the angle. This is the same as going around a complete circle and ending up where you started. In the above root:
This gives another, equally valid root of the number. In fact, any number other than {\mathbf 0} has \(r\) \(r\)th roots. These roots will be evenly divided across the full range of \(2\pi\). They will all have the same magnitude. You can draw a circle with a radius of the \(r\)th root of \(n\) and it will pass through all \(r\) roots of {\mathbf n}.
Example 1
Find all the cube roots of \(1+j0\). Since the magnitude of this number is 1 and the direction is 0, the first cube root has a magnitude of \(1^{\frac{1}{3}}=1\) and a direction of \(0/3=0\). Since the roots are equally spaced, they will be \(\frac{2\pi}{3}\,\!\) apart, meaning:
Example 2
Find all the fifth roots of \({\mathbf n}=8-j6\).
First, find the magnitude and direction:
The magnitude and direction of the primary root \({\mathbf q_1}\) will therefore be:
In its rectangular representation, this is:
The next four roots will be evenly spaced around the complex plane, so they will be \(\frac{2\pi}{5}\,\!\) apart and have directions of:
By converting from Euler to rectangular notation, you can find:
These are shown in the figure at right.
Non-integer Powers
Non-integer powers and roots are more complicated. If you are only looking for the primary power for any arbitrary scalar a then you can simply calculate:
For rational powers (powers that can be represented by a fraction), you can first raise the complex number to the numerator and then take roots from the denominator. That is:
Parting Thoughts
Decide early on a notation you like for complex numbers. Some possibilities are:
For example, using complex variables to give Ohm's Law might look like:
Make sure you know how your angles are represented (degrees or radians). If someone asks you "What is the cosine of 45," you need to start getting the the habit of asking "radians or degrees?" even though it may seem obvious. Also, if someone says "the frequency is ten," you need to always ask "in Hertz or radians per second?"
Complex numbers are at the heart of many powerful tools in engineering. You need to be comfortable with how complex numbers work and what they represent in order to truly understand how those tools work and to fully comprehend their usefulness. Complex numbers are not that difficult once you have practiced with them a little bit, and the time spent learning about them will pay great dividends in the future.
- ↑ Physics Web, accessed October 12, 2006