Difference between revisions of "Simulink/Tutorials/Nise8"
Jump to navigation
Jump to search
| Line 108: | Line 108: | ||
save_system(Filename) | save_system(Filename) | ||
%close_system(Filename) | %close_system(Filename) | ||
| − | <syntaxhighlight> | + | </syntaxhighlight> |
== Second Order Differential Equation == | == Second Order Differential Equation == | ||
Latest revision as of 20:31, 16 July 2020
The models and codes below were made in MATLAB R2020a and are available at the Summer Controls Simulink Folder
Contents
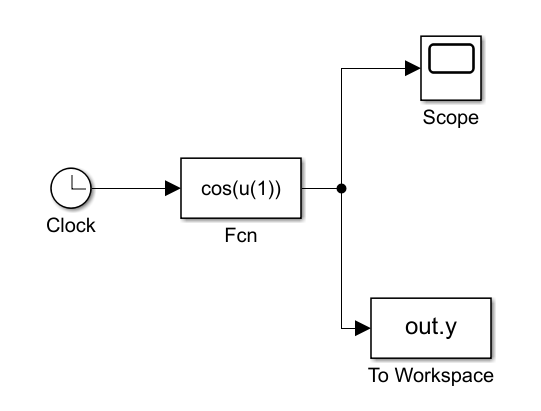
Simple Simulation
Model
Code
%% Startup
clear
format short e
%% Define filename
Filename = 'SimLabWithScript'
open_system(Filename)
%% Get info about the model
get_param(Filename, 'ObjectParameters')
%% Set typical parameters
% Solver
%%% Simulation time
set_param(Filename, 'StartTime', '0')
set_param(Filename, 'StopTime', '10')
%%% Solver options
set_param(Filename, 'Solver', 'ode45')
set_param(Filename, 'MaxStep', 'auto')
set_param(Filename, 'MinStep', 'auto')
set_param(Filename, 'InitialStep', 'auto')
set_param(Filename, 'RelTol', '1e-3')
set_param(Filename, 'AbsTol', 'auto')
%% Data Import/Export
%%% Save options
set_param(Filename, 'LimitDataPoints', 'off')
%% Get info about the blocks
get_param([Filename '/Clock'], 'ObjectParameters')
get_param([Filename '/Fcn'], 'ObjectParameters')
get_param([Filename '/Scope'], 'ObjectParameters')
get_param([Filename '/To Workspace'], 'ObjectParameters')
get_param([Filename '/To Workspace'], 'VariableName')
%% Set function block info
set_param([Filename '/Fcn'], 'Expression', 'cos(u(1))')
%% Run the system
out = sim(Filename)
%% Plot the data
plot(out.tout, out.y, 'ko:')
%% Save plot, model image, and model based on filename
eval(sprintf('print -deps %sout', Filename))
%eval(sprintf('print -s%s -deps %smodel', Filename, Filename))
save_system(Filename)
% close_system(Filename)
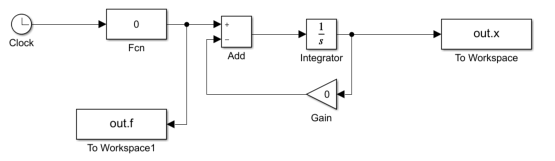
First Order Differential Equation
Model
Code
% Startup
clear
format short e
% Define filename
Filename = 'FirstDeriv'
open_system(Filename)
% Set typical parameters
%% Solver
%%% Simulation time
set_param(Filename, 'StartTime', '0')
set_param(Filename, 'StopTime', '10')
%%% Solver options
set_param(Filename, 'Solver', 'ode45')
set_param(Filename, 'MaxStep', 'auto')
set_param(Filename, 'MinStep', 'auto')
set_param(Filename, 'InitialStep', 'auto')
set_param(Filename, 'RelTol', '1e-3')
set_param(Filename, 'AbsTol', 'auto')
%% Data Import/Export
%%% Save options
set_param(Filename, 'LimitDataPoints', 'off')
% Set function block info
set_param([Filename '/Fcn'], 'Expression', '0')
set_param([Filename '/Gain'], 'Gain', '0')
set_param([Filename '/Integrator'], 'InitialCondition', '0')
% Run the system
out = sim(Filename)
% Plot the data
figure(1); clf
plot(out.tout, out.f, 'k-', out.tout, out.x, 'r-')
gzoom
title('Input and Response for FD')
xlabel('Time (s)');
ylabel('Value');
legend('Input', 'Output', 'location', 'best')
% Save plot, model image, and model based on filename
eval(sprintf('print -deps %sout', Filename))
eval(sprintf('print -s%s -dpng %smodel', Filename, Filename))
save_system(Filename)
%close_system(Filename)
Second Order Differential Equation
Model
Code
% Startup
clear
format short e
% Define filename
Filename = 'SecondDeriv'
open_system(Filename)
% Set typical parameters
%% Solver
%%% Simulation time
set_param(Filename, 'StartTime', '0')
set_param(Filename, 'StopTime', '10')
%%% Solver options
set_param(Filename, 'Solver', 'ode45')
set_param(Filename, 'MaxStep', 'auto')
set_param(Filename, 'MinStep', 'auto')
set_param(Filename, 'InitialStep', 'auto')
set_param(Filename, 'RelTol', '1e-3')
set_param(Filename, 'AbsTol', 'auto')
%% Data Import/Export
%%% Save options
set_param(Filename, 'LimitDataPoints', 'off')
% Set function block info
set_param([Filename '/Fcn'], 'Expression', '0')
set_param([Filename '/Gain'], 'Gain', '0')
set_param([Filename '/Gain1'], 'Gain', '0')
set_param([Filename '/Integrator'], 'InitialCondition', '0')
set_param([Filename '/Integrator1'], 'InitialCondition', '0')
% Run the system
out = sim(Filename)
% Plot the data
figure(1); clf
plot(out.tout, out.f, 'k-', out.tout, out.x, 'r-')
gzoom
title('Input and Response for SD')
xlabel('Time (s)');
ylabel('Value');
legend('Input', 'Output', 'location', 'best')
% Save plot, model image, and model based on filename
eval(sprintf('print -deps %sout', Filename))
eval(sprintf('print -s%s -dpng %smodel', Filename, Filename))
save_system(Filename)
%close_system(Filename)