Difference between revisions of "EGR 103/Concept List/F21"
Jump to navigation
Jump to search
\(
y=e^x=\sum_{n=0}^{\infty}\frac{x^n}{n!}
\)
\(
\begin{align}
y_{init}&=1\\
y_{new}&=y_{old}+\frac{x^n}{n!}
\end{align}
\)
| (One intermediate revision by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | == Lecture 1 - Course Introduction == | + | == Lecture 1 - 8/23 - Course Introduction == |
* Main class page: [http://classes.pratt.duke.edu/EGR103F21/ EGR 103L]. | * Main class page: [http://classes.pratt.duke.edu/EGR103F21/ EGR 103L]. | ||
* See information on PDF of slide show on [http://classes.pratt.duke.edu/EGR103F21/errataetc.html Errata / Notes] page. | * See information on PDF of slide show on [http://classes.pratt.duke.edu/EGR103F21/errataetc.html Errata / Notes] page. | ||
| Line 6: | Line 6: | ||
* CampusWire page: [https://campuswire.com/c/GCCD2906F/feed CampusWire 103L page]; message board for questions - you need to be in the class and have the access code 8018 to subscribe. | * CampusWire page: [https://campuswire.com/c/GCCD2906F/feed CampusWire 103L page]; message board for questions - you need to be in the class and have the access code 8018 to subscribe. | ||
| − | == Lecture 2 - Programs and Programming == | + | == Lecture 2 - 8/27 - Programs and Programming == |
* Almost all languages have input, output, math, conditional execution (decisions), and repetition (loops) | * Almost all languages have input, output, math, conditional execution (decisions), and repetition (loops) | ||
* Seven steps of programming [https://adhilton.pratt.duke.edu/sites/adhilton.pratt.duke.edu/files/u37/iticse-7steps.pdf The Seven Steps Poster] | * Seven steps of programming [https://adhilton.pratt.duke.edu/sites/adhilton.pratt.duke.edu/files/u37/iticse-7steps.pdf The Seven Steps Poster] | ||
| Line 26: | Line 26: | ||
** <code>NUM = int(VAR)</code> will convert the item in VAR to an integer if it looks like an integer; error otherwise | ** <code>NUM = int(VAR)</code> will convert the item in VAR to an integer if it looks like an integer; error otherwise | ||
| − | == Lecture 3 - "Number" Types == | + | == Lecture 3 - 8/30 - "Number" Types == |
* Finished prime number checker - code is available in the Box drive for the class under Lectures / Lec03 | * Finished prime number checker - code is available in the Box drive for the class under Lectures / Lec03 | ||
** Looked at for loops for running code multiple times | ** Looked at for loops for running code multiple times | ||
| Line 64: | Line 64: | ||
** Only works for arrays! | ** Only works for arrays! | ||
| − | == Lecture 4 - Other Types == | + | == Lecture 4 - 9/3 - Other Types == |
* Lists are set off with [ ] and entries can be any valid type (including other lists!); entries can be of different types from other entries; list items can be changed and mutable items within lists can be changed. Lists can be "grown" by using += with the list. | * Lists are set off with [ ] and entries can be any valid type (including other lists!); entries can be of different types from other entries; list items can be changed and mutable items within lists can be changed. Lists can be "grown" by using += with the list. | ||
* Tuples are indicated by commas without square brackets (and are usually shown with parentheses - which are required if trying to make a tuple an entry in a tuple or a list); tuple items cannot be changed but mutable items within tuples can be | * Tuples are indicated by commas without square brackets (and are usually shown with parentheses - which are required if trying to make a tuple an entry in a tuple or a list); tuple items cannot be changed but mutable items within tuples can be | ||
| Line 90: | Line 90: | ||
** [https://www.tutorialspoint.com/python/python_tuples.htm Tuples] at tutorialspoint | ** [https://www.tutorialspoint.com/python/python_tuples.htm Tuples] at tutorialspoint | ||
| − | == Lecture 5 - Format and Functions == | + | == Lecture 5 - 9/6 - Format and Functions == |
* Creating formatted strings using {} and .format() ([https://www.python.org/dev/peps/pep-3101/#format-strings format strings], [https://www.python.org/dev/peps/pep-3101/#standard-format-specifiers standard format specifiers]) -- focus was on using s for string and e or f for numerical types, minimumwidth.precision, and possibly a + in front to force printing + for positive numbers. | * Creating formatted strings using {} and .format() ([https://www.python.org/dev/peps/pep-3101/#format-strings format strings], [https://www.python.org/dev/peps/pep-3101/#standard-format-specifiers standard format specifiers]) -- focus was on using s for string and e or f for numerical types, minimumwidth.precision, and possibly a + in front to force printing + for positive numbers. | ||
** Using {} by themselves will substitute items in order from the <code>format()</code> function into the string that gets created | ** Using {} by themselves will substitute items in order from the <code>format()</code> function into the string that gets created | ||
| Line 119: | Line 119: | ||
** If there is a left side to the function call, it either needs to be a single variable name or a tuple with as many entries as the number of items returned | ** If there is a left side to the function call, it either needs to be a single variable name or a tuple with as many entries as the number of items returned | ||
| − | == Lecture 6 - Relational Operators, Decisions, and Loops == | + | == Lecture 6 - 9/10 - Relational Operators, Decisions, and Loops == |
* <= < == >= > != work with many types; just be careful about interpreting | * <= < == >= > != work with many types; just be careful about interpreting | ||
* <code>not</code> can reverse while <code>and</code> and <code>or</code> can combine logical expressions | * <code>not</code> can reverse while <code>and</code> and <code>or</code> can combine logical expressions | ||
| Line 132: | Line 132: | ||
* The Price Is Right game! | * The Price Is Right game! | ||
| − | == Lecture 7 - More Loops and Logical Masks == | + | == Lecture 7 - 9/13 - More Loops and Logical Masks == |
* Using a list to keep track of counts | * Using a list to keep track of counts | ||
* Using the <code>enumerate</code> type to provide a collection of indices and values to a loop | * Using the <code>enumerate</code> type to provide a collection of indices and values to a loop | ||
* Basics of [[Python:Logical Masks]] | * Basics of [[Python:Logical Masks]] | ||
| − | == Lecture 8 - Dictionaries == | + | == Lecture 8 - 9/17 - Dictionaries == |
* Dictionaries are collections of key : value pairs set off with { }; keys can be any immutable type (int, float, string, tuple) and must be unique; values can be any type and do not need to be unique | * Dictionaries are collections of key : value pairs set off with { }; keys can be any immutable type (int, float, string, tuple) and must be unique; values can be any type and do not need to be unique | ||
** [https://www.tutorialspoint.com/python/python_dictionary.htm Dictionary] at tutorialspoint | ** [https://www.tutorialspoint.com/python/python_dictionary.htm Dictionary] at tutorialspoint | ||
| Line 144: | Line 144: | ||
* Translation demo with Morse code and NATO phonetic alphabet | * Translation demo with Morse code and NATO phonetic alphabet | ||
| − | == Lecture 9 - Iterative Methods == | + | == Lecture 9 - 9/20 - Iterative Methods == |
* Taylor series fundamentals | * Taylor series fundamentals | ||
* Maclaurin series approximation for exponential uses Chapra 4.2 to compute terms in an infinite sum. | * Maclaurin series approximation for exponential uses Chapra 4.2 to compute terms in an infinite sum. | ||
| Line 166: | Line 166: | ||
</math> | </math> | ||
* See Python version of Fig. 4.2 and modified version of 4.2 in the Resources section of Sakai page under Chapra Pythonified | * See Python version of Fig. 4.2 and modified version of 4.2 in the Resources section of Sakai page under Chapra Pythonified | ||
| + | |||
| + | == Lecture 10 - 9/24 - Binary == | ||
| + | * Different number systems convey information in different ways. | ||
| + | ** Roman Numerals | ||
| + | ** Chinese Numbers | ||
| + | ** Binary Numbers | ||
| + | *** We went through how to convert between decimal and binary | ||
| + | * Floats (specifically double precision floats) are stored with a sign bit, 52 fractional bits, and 11 exponent bits. The exponent bits form a code: | ||
| + | ** 0 (or 00000000000): the number is either 0 or a denormal | ||
| + | ** 2047 (or 11111111111): the number is either infinite or not-a-number | ||
| + | ** Others: the power of 2 for scientific notation is 2**(code-1023) | ||
| + | *** The largest number is thus just *under* 2**1024 (ends up being (2-2**-52)**1024<math>\approx 1.798\times 10^{308}</math>. | ||
| + | *** The smallest normal number (full precision) is 2**(-1022)<math>\approx 2.225\times 10^{-308}</math>. | ||
| + | *** The smallest denormal number (only one significant binary digit) is 2**(-1022)/2**53 or 5e-324. | ||
| + | ** When adding or subtracting, Python can only operate on the common significant digits - meaning the smaller number will lose precision. | ||
| + | ** (1+1e-16)-1=0 and (1+1e-15)-1=1.1102230246251565e-15 | ||
| + | ** Avoid intermediate calculations that cause problems: if x=1.7e308, | ||
| + | *** (x+x)/x is inf | ||
| + | *** x/x + x/x is 2.0 | ||
| + | ** $$e^x=\lim_{n\rightarrow \infty}\left(1+\frac{x}{n}\right)^n$$ | ||
| + | <div class="mw-collapsible mw-collapsed"> | ||
| + | <source lang=python> | ||
| + | # Exponential Demo | ||
| + | </source> | ||
| + | <div class="mw-collapsible-content"> | ||
| + | <syntaxhighlightlang=python> | ||
| + | import numpy as np | ||
| + | import matplotlib.pyplot as plt | ||
| + | |||
| + | def exp_calc(x, n): | ||
| + | return (1 + x/n)**n | ||
| + | |||
| + | if __name__ == "__main__": | ||
| + | n = np.logspace(0, 17, 1000) | ||
| + | y = exp_calc(1, n) | ||
| + | fig, ax = plt.subplots(num=1, clear=True) | ||
| + | ax.semilogx(n, y) | ||
| + | fig.savefig('ExpDemoPlot1.png') | ||
| + | |||
| + | # Focus on right part | ||
| + | n = np.logspace(13, 16, 1000) | ||
| + | y = exp_calc(1, n) | ||
| + | fig, ax = plt.subplots(num=2, clear=True) | ||
| + | ax.semilogx(n, y) | ||
| + | fig.savefig('ExpDemoPlot2.png') | ||
| + | </syntaxhighlight> | ||
| + | </div> | ||
| + | </div> | ||
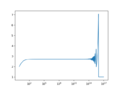
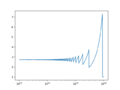
| + | <gallery> | ||
| + | File:ExpDemoPlot1.png|estimates for calculating $$e$$ with $$n$$ between 1 and $$1*10^{17}$$ | ||
| + | File:ExpDemoPlot2.png|$$n$$ between $$10^{13}$$ and $$10^{16}$$ showing region when roundoff causes problems | ||
| + | </gallery> | ||
| + | |||
| + | * Want to see Amharic? | ||
| + | list(map(chr, range(4608, 4992))) | ||
| + | * Want to see the Greek alphabet? | ||
| + | <syntaxhighlight lang=python> | ||
| + | for k in range(913,913+25): | ||
| + | print(chr(k), chr(k+32)) | ||
| + | </syntaxhighlight> | ||
| + | |||
| + | == Lecture 11 - 9/27 - Monte Carlo Methods == | ||
| + | * From Wikipedia: [https://en.wikipedia.org/wiki/Monte_Carlo_method Monte Carlo method] | ||
| + | * Walker demo | ||
| + | <html><iframe src="https://trinket.io/embed/python3/e1a9a460b1" width="100%" height="600" frameborder="0" marginwidth="0" marginheight="0" allowfullscreen></iframe></html> | ||
| + | |||
| + | == Lecture 12 - 10/1 - Matrices and Matrix Operations == | ||
| + | * 1D arrays are neither rows nor columns - they are 1D! | ||
| + | * 2D arrays have...two dimensions, one of which might be 1 | ||
| + | ** Python does mathematical operations differently for 1 and 2-D arrays | ||
| + | * Dot products as heart of matrix multiplication | ||
| + | ** Inner dimensions must match; outer dimensions equal dimensions of result | ||
| + | * To multiply matrices A and B ($$C=A\times B$$ in math or <code>C=A@B</code> in Python) using matrix multiplication, the number of columns of A must match the number of rows of B; the results will have the same number of rows as A and the same number of columns as B. '''Order is important''' | ||
| + | * Matrix multiplication (by hand) | ||
| + | * Matrix multiplication (using @ in Python) | ||
| + | * Reformatting linear algebra expressions as matrix equations | ||
| + | * Calculating determinants and inverses | ||
| + | * Determinants of matrices and the meaning when the determinant is 0 | ||
| + | ** Shortcuts for determinants of 1x1, 2x2 and 3x3 matrices (see class notes for processes) | ||
| + | ::$$\begin{align*} | ||
| + | \mbox{det}([a])&=a\\ | ||
| + | \mbox{det}\left(\begin{bmatrix}a&b\\c&d\end{bmatrix}\right)&=ad-bc\\ | ||
| + | \mbox{det}\left(\begin{bmatrix}a&b&c\\d&e&f\\g&h&i\end{bmatrix}\right)&=aei+bfg+cdh-afh-bdi-ceg\\ | ||
| + | \end{align*}$$ | ||
| + | :* Don't believe me? Ask [https://www.youtube.com/watch?v=ROFcVgehEYA Captain Matrix]! | ||
| + | * Inverses of matrices: | ||
| + | ** Generally, $$\mbox{inv}(A)=\frac{\mbox{cof}(A)^T}{\mbox{det}(A)}$$ there the superscript T means transpose... | ||
| + | *** And $$\mbox{det}(A)=\sum_{i\mbox{ or }j=0}^{N-1}a_{ij}(-1)^{i+j}M_{ij}$$ for some $$j$$ or $$i$$... | ||
| + | **** And $$M_{ij}$$ is a '''minor''' of $$A$$, specifically the determinant of the matrix that remains if you remove the $$i$$th row and $$j$$th column or, if $$A$$ is a 1x1 matrix, 1 | ||
| + | ***** And $$\mbox{cof(A)}$$ is a matrix where the $$i,j$$ entry $$c_{ij}=(-1)^{i+j}M_{ij}$$ | ||
| + | ** Good news - for this class, you need to know how to calculate inverses of 1x1 and 2x2 matrices only: | ||
| + | :: $$ | ||
| + | \begin{align} | ||
| + | \mbox{inv}([a])&=\frac{1}{a}\\ | ||
| + | \mbox{inv}\left(\begin{bmatrix}a&b\\c&d\end{bmatrix}\right)&=\frac{\begin{bmatrix}d &-b\\-c &a\end{bmatrix}}{ad-bc} | ||
| + | \end{align}$$ | ||
| + | |||
| + | == Lecture 13 - 10/18 - Office Hours == | ||
| + | * Office Hours | ||
| + | |||
| + | == Lecture 14 - 10/11 - Norms and Condition Numbers == | ||
| + | * Chapra 11.2.1 for norms | ||
| + | ** [https://docs.scipy.org/doc/numpy/reference/generated/numpy.linalg.norm.html np.linalg.norm()] in Python | ||
| + | * Chapra 11.2.2 for condition numbers | ||
| + | ** [https://docs.scipy.org/doc/numpy/reference/generated/numpy.linalg.norm.html np.linalg.cond()] in Python | ||
| + | ** Note: base-10 logarithm of condition number gives number of digits of precision possibly lost due to system geometry and scaling (top of p. 295 in Chapra) | ||
| + | |||
| + | == Lecture 15 - 10/15 - 3D Plotting == | ||
| + | * subplots | ||
| + | * [[Python:Plotting Surfaces]] | ||
| + | |||
| + | == Lecture 16 - 10/18 - Statistics and Curve Fitting I == | ||
| + | * Definition of curve fitting versus interpolation: | ||
| + | ** Curve fitting involves taking a scientifically vetted model, finding the best coefficients, and making predictions based on the model. The model may not perfectly hit any of the actual data points. | ||
| + | ** Interpolation involves making a guess for values between data points. Interpolants actually hit all the data points but may have no scientific validity at all. Interpolation is basically "connecting the dots," which may involve mathematically complex formulae. | ||
| + | * Statistical definitions used (see [[Statistics Symbols]] for full list): | ||
| + | ** $$x$$ will be used for independent data | ||
| + | ** $$y$$ will be used for dependent data | ||
| + | ** $$\bar{x}$$ and $$\bar{y}$$ will be used for the averages of the $$x$$ and $$y$$ sets | ||
| + | ** $$\hat{y}_k$$ will be used for the estimate of the $$k$$th dependent point | ||
| + | ** $$S_t=\sum_k\left(y_k-\bar{y}\right)^2$$ is the sum of the squares of the data residuals and gives a measure of the spread of the data though any given value can mean several different things for a data set. It will be a non-negative number; a value of 0 implies all the $$y$$ values are the same. | ||
| + | ** $$S_r=\sum_k\left(y_k-\hat{y}_k\right)^2$$ is the sum of the squares of the estimate residuals and gives a measure of the collective distance between the data points and the model equation for the data points. It will be a non-negative number; a value of 0 implies all the estimates are mathematically perfectly predicted by the model. | ||
| + | ** $$r^2=\frac{S_t-S_r}{S_t}=1-\frac{S_r}{S_t}$$ is the coefficient of determination; it is a normalized value that gives information about how well a model predicts the data. An $$r^2$$ value of 1 means the model perfectly predicted every value in the data set. A value of 0 means the model does as well as having picked the average. A negative value means the model is '''worse''' than merely picking the average. | ||
| + | * Mathematical proof of solution to [[General Linear Regression]] | ||
| + | * [[Python:Fitting]] | ||
| + | |||
| + | == Lecture 17 - 10/22 - Statistics and Curve Fitting II == | ||
| + | * Linear versus Nonlinear Fits | ||
| + | * Clarification on how general linear regression works | ||
| + | |||
| + | == Lecture 18 - 10/25 - Statistics and Curve Fitting III == | ||
| + | * Walkthrough of a general linear fit | ||
| + | * args in function definitions and their usefulness | ||
| + | * Non-linear models | ||
| + | * [[Python:Fitting#Nonlinear_Regression]] | ||
| + | |||
| + | == Lecture 19 - 10/29 - Finding Roots == | ||
| + | * [[Python:Finding roots]] | ||
| + | * SciPy references (all from [https://docs.scipy.org/doc/scipy/reference/optimize.html Optimization and root finding]): | ||
| + | ** [https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.brentq.html scipy.optimize.brentq] - closed method root finding | ||
| + | ** [https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.fsolve.html scipy.optimize.fsolve] - open method root finding | ||
| + | |||
| + | == Lecture 20 - 11/1 - Finding Extrema == | ||
| + | * [[Python:Extrema]] | ||
| + | * SciPy references (all from [https://docs.scipy.org/doc/scipy/reference/optimize.html Optimization and root finding]): | ||
| + | ** [https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.fmin.html scipy.optimize.fmin] - unbounded minimization | ||
| + | ** [https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.fminbound.html scipy.optimize.fminbound] - bounded minimization | ||
| + | |||
| + | == Lecture 21 - 11/5 - Interpolation == | ||
| + | * [[Python:Interpolation]] | ||
| + | * Interpolations are meant to estimate values between points in a data set. | ||
| + | * Interpolants must go through all the data points - different concept from a fit; also interpolation functions generally have different coefficients for the interpolant between every pair of points - very different from a fit | ||
| + | * Unlike a model, the functions used to interpolate may have no scientific validity; instead, they satisfy different mathematical conditions. | ||
| + | * The main interpolations we looked at are nearest neighbor, linear, and cubic spline with different conditions (not-a-knot, clamped, natural) | ||
| + | ** Most basic interpolation simply looks at most recent value of data (i.e. data point "to the left") | ||
| + | ** Next most basic is nearest neighbor - closest point | ||
| + | ** Next is linear interpolation - straight line between neighboring points | ||
| + | ** After that, using third-order polynomials is common | ||
| + | |||
| + | == Lecture 22 - 11/8 - Zips, Maps, and Filters == | ||
| + | * Maps, filters, zips create a '''one-time-use''' iterable type | ||
| + | ** map(FUN, ITERABLE) applies a function to each element in an iterable and returns an iterable | ||
| + | ** filter(FUN, ITERABLE) applies a logical expression to each element and includes that element in the return only if the function is true | ||
| + | ** zip(A, B) takes corresponding elements from A and B and returns an iterable made up of tuples with the corresponding elements from A and B | ||
| + | *** Very useful for making a dictionary out of a collection of keys and a collection of values | ||
| + | * List comprehensions | ||
| + | ** [FUNCTION for VAR in SEQUENCE if LOGIC] | ||
| + | *** The FUNCTION should return a single thing (though that thing can be a list, tuple, etc) | ||
| + | *** The "if LOGIC" part is optional | ||
| + | *** <code>[k for k in range(3)]</code> creates <code>[0, 1, 2]</code> | ||
| + | *** <code>[k**2 for k in range (5, 8)]</code> creates <code>[25, 36, 49]</code> | ||
| + | *** <code>[k for k in 'hello' if k<'i']</code> creates <code>['h', 'e']</code> | ||
| + | *** <code>[(k,k**2) for k in range(11) if k%3==2]</code> creates <code>[(2, 4), (5, 25), (8, 64)]</code> | ||
| + | * Scrabble example | ||
| + | |||
| + | == Lecture 23 - 11/12 - Class Cancelled == | ||
| + | |||
| + | == Lecture 24 - 11/15 - Numerical Integartion and Differentiation I == | ||
| + | * Newton Interpolating Polynomials | ||
| + | * Overview of integration | ||
| + | ** Riemann sums | ||
| + | ** Trapezoidal Rule | ||
| + | ** Simpson's 1/3 and 3/8 Rules | ||
| + | * Overview of differentiation | ||
| + | ** 2pt forward first derivative | ||
| + | *** Exception at first point | ||
| + | ** 2 pt backward first derivative | ||
| + | *** Exception at last point | ||
| + | ** 3pt centered first derivative | ||
| + | *** Exceptions at first and last points | ||
| + | ** 3pt centered second derivative | ||
| + | *** Exceptions at first and last points | ||
| + | |||
| + | == Lecture 25 - 11/9 - Numerical Integartion and Differentiation II == | ||
| + | * Working examples by hand | ||
| + | * Writing code for some of the above | ||
| + | |||
| + | == Lecture 26 - 11/22 - Office Hours == | ||
| + | |||
| + | == Lecture 27 - 11/29 - Initial Value Problems == | ||
| + | * Introduction to IVP where $$\frac{dy}{dt}=f(t, y, C)$$ and $$y_0$$ is known | ||
| + | * Overview of particular and homogeneous solutions | ||
| + | * Euler-Cauchy method | ||
| + | * Runge-Kutta 4 | ||
| + | * [[Python:Ordinary Differential Equations]] | ||
| + | |||
| + | == Lecture 28 - 12/3 - Classes in Python == | ||
Latest revision as of 19:56, 2 December 2021
Contents
- 1 Lecture 1 - 8/23 - Course Introduction
- 2 Lecture 2 - 8/27 - Programs and Programming
- 3 Lecture 3 - 8/30 - "Number" Types
- 4 Lecture 4 - 9/3 - Other Types
- 5 Lecture 5 - 9/6 - Format and Functions
- 6 Lecture 6 - 9/10 - Relational Operators, Decisions, and Loops
- 7 Lecture 7 - 9/13 - More Loops and Logical Masks
- 8 Lecture 8 - 9/17 - Dictionaries
- 9 Lecture 9 - 9/20 - Iterative Methods
- 10 Lecture 10 - 9/24 - Binary
- 11 Lecture 11 - 9/27 - Monte Carlo Methods
- 12 Lecture 12 - 10/1 - Matrices and Matrix Operations
- 13 Lecture 13 - 10/18 - Office Hours
- 14 Lecture 14 - 10/11 - Norms and Condition Numbers
- 15 Lecture 15 - 10/15 - 3D Plotting
- 16 Lecture 16 - 10/18 - Statistics and Curve Fitting I
- 17 Lecture 17 - 10/22 - Statistics and Curve Fitting II
- 18 Lecture 18 - 10/25 - Statistics and Curve Fitting III
- 19 Lecture 19 - 10/29 - Finding Roots
- 20 Lecture 20 - 11/1 - Finding Extrema
- 21 Lecture 21 - 11/5 - Interpolation
- 22 Lecture 22 - 11/8 - Zips, Maps, and Filters
- 23 Lecture 23 - 11/12 - Class Cancelled
- 24 Lecture 24 - 11/15 - Numerical Integartion and Differentiation I
- 25 Lecture 25 - 11/9 - Numerical Integartion and Differentiation II
- 26 Lecture 26 - 11/22 - Office Hours
- 27 Lecture 27 - 11/29 - Initial Value Problems
- 28 Lecture 28 - 12/3 - Classes in Python
Lecture 1 - 8/23 - Course Introduction
- Main class page: EGR 103L.
- See information on PDF of slide show on Errata / Notes page.
- Sakai page: Sakai 103L page; grades, surveys and tests, some assignment submissions
- Pundit page: EGR 103; reference lists
- CampusWire page: CampusWire 103L page; message board for questions - you need to be in the class and have the access code 8018 to subscribe.
Lecture 2 - 8/27 - Programs and Programming
- Almost all languages have input, output, math, conditional execution (decisions), and repetition (loops)
- Seven steps of programming The Seven Steps Poster
- Watch video on Developing an Algorithm
- Watch video on A Seven Step Approach to Solving Programming Problems
- Consider how to decide if a number is a prime number
- To play with Python:
- Install it on your machine or a public machine: Download
- Quick tour of Python
- Editing window, variable explorer, and console
- Main numerical types: whole numbers (int) and numbers with decimals (float)
- + - * // (rounded division) and % (remainder / modula) produce in if both sides are an int, float if either or both are floats
- / (regular division) and // (rounded division) produces float with ints or floats
- ** to do powers
- Python doesn't know everything to start with; may need to import things
import MODULEmeans usingMODULE.function()to runimport MODULE as NAMEmeans usingNAME.function()to run
VAR = input("prompt: ")will ask the user for a value and stores whatever they type as a stringNUM = int(VAR)will convert the item in VAR to an integer if it looks like an integer; error otherwise
Lecture 3 - 8/30 - "Number" Types
- Finished prime number checker - code is available in the Box drive for the class under Lectures / Lec03
- Looked at for loops for running code multiple times
- Looked at if...else trees for making decisions
- Created a variable to track whether we thought the number was prime
- Python is a "typed" language - variables have types. We will use several types:
- Focus of the day: int, float, and array
- Focus a little later: string, list, tuple
- Focus later: dictionary, set
- Focus way later: map, filter, zip
- int: integers; Python 3 can store these perfectly
- float: floating point numbers - "numbers with decimal points" - Python sometimes has problems storing floating point items exactly
- array
- Requires numpy, usually with
import numpy as np - Organizational unit for storing rectangular arrays of numbers
- Generally create with np.array(LIST) where depth of nested LIST is dimensionality of array
- np.array([1, 2, 3]) is a 1-dimensional array with 3 elements
- np.array([[1, 2, 3], [4, 5, 6]]) is a 2-dimension array with 2 rows and 3 columns
- Requires numpy, usually with
- Math with "Number" types works the way you expect
- ** * / // % + -
- With arrays, * and / work element by element; *matrix* multiplication is a different character (specifically, @)
- Relational operators can compare "Number" Types and work the way you expect with True or False as an answer
- < <= == >= > !=
- With arrays, either same size or one is a single value; result will be an array of True and False the same size as the array
- Slices allow us to extract information from a collection or change information in mutable collections
- a[0] is the element in a at the start
- a[3] is the element in a three away from the start
- a[-1] is the last element of a
- a[-2] is the second-to-last element of a
- a[:] is all the elements in a because what is really happening is:
- a[start:until] where start is the first index and until is just *past* the last index;
- a[3:7] will return a[3] through a[6] in a 4-element array
- a[start:until:increment] will skip indices by increment instead of 1
- To go backwards, a[start:until:-increment] will start at an index and then go backwards until getting at or just past until.
- For 2-D arrays, you can index items with either separate row and column indices or indices separated by commas:
- a[2][3] is the same as a[2, 3]
- Only works for arrays!
Lecture 4 - 9/3 - Other Types
- Lists are set off with [ ] and entries can be any valid type (including other lists!); entries can be of different types from other entries; list items can be changed and mutable items within lists can be changed. Lists can be "grown" by using += with the list.
- Tuples are indicated by commas without square brackets (and are usually shown with parentheses - which are required if trying to make a tuple an entry in a tuple or a list); tuple items cannot be changed but mutable items within tuples can be
- Strings are set off with " " or ' ' and contain characters; string items cannot be changed
- For lists, tuples, and strings:
- Using + concatenates the two collections
- Using * with them makes creates a collection with the orignal repeated that many times
- Using += will create a new item with something appended to the old item; the "something" needs to be the same type (list, tuple, or string); this may seem to break the "can't be changed" rule but really
a += bisa = a + bwhich creates a newa.
- Characters in strings have "numerical" values based on the ASCII table (https://www.asciitable.com/)
- Numbers are earlier than lower case letters; lower case letters are earlier than upper case letters
- Strings are sorted character by character; if one string is shorter than another, it is considered less
- " Hello" < "Hi" since the "e" comes before the "i"
- "Zebra" < "apple" since the upper case "Z" is before the lower case "a"
- "go" < "gone" since the first two characters match and then the word is done
- To get the numerical value of a single character, use
ord("A")or replace the A with the character you want - To get the character a number represents, use
chr(NUM) - To apply either ord or chr to multiple items, use a
map; to see the results, make alistout of the map - Trinket
- To read more:
Lecture 5 - 9/6 - Format and Functions
- Creating formatted strings using {} and .format() (format strings, standard format specifiers) -- focus was on using s for string and e or f for numerical types, minimumwidth.precision, and possibly a + in front to force printing + for positive numbers.
- Using {} by themselves will substitute items in order from the
format()function into the string that gets created - Putting a number in the {} will tell
formatwhich thing to get - Format specification comes after a : in the {}; if you do not specify a location index, you still have to put a colon in the {}
- {:s} means string and {:Xs} where X is an integer means reserve at least that much space for a left-formatted string
- {:f} means floating point (default 6 digits after decimal point) and {:X.Yf} reserves at least X spaces (including + or - and the . if it is there) with Y digits after the decimal point for t right-justified number
- {:e} means floating point (default 6 digits after decimal point) and {:X.Ye} reserves at least X spaces (including + or - and the . if it is there and the letter e and the + or - after the e and the two or three digit number after that) with Y digits after the decimal point for t right-justified number
- Using {} by themselves will substitute items in order from the
- Aside - Format Specification Mini-Language has all the possibilities; we will cover some but not all of these in later classes
- You can enter numbers in scientific notation with a number followed by the letter 3 and then a number or negative number for the power of 10; for example,
x = 6.02e23ore = -1.6e-19- float can convert scientific notation as well:
float("1e-5")
- Defined functions can be multiple lines of code and have multiple outputs.
def FNAME(local1, local2, ...): CODE return THING1, THING2, ...
- Four different types of input parameters - we only really talked about the first kind:
- Required (listed first)
- We will cover the other kinds later
- Named with defaults (second)
- Additional positional arguments ("*args") (third)
- Function will create a tuple containing these items in order
- Additional keyword arguments ("**kwargs") (last)
- Function will create a dictionary of keyword and value pairs
- Function ends when indentation stops or when the function hits a return statement
- Return returns single item as an item of that type; if there are multiple items returned, they are stored and returned in a tuple
- If there is a left side to the function call, it either needs to be a single variable name or a tuple with as many entries as the number of items returned
- Four different types of input parameters - we only really talked about the first kind:
Lecture 6 - 9/10 - Relational Operators, Decisions, and Loops
- <= < == >= > != work with many types; just be careful about interpreting
notcan reverse whileandandorcan combine logical expressions- Basics of decisions using if...elif...else
- Must have logic after if
- Can have as many elif with logic after
- Can have an else without logic at the end
- Flow is solely dependent on indentation!
- Branches can contain other trees for follow-up questions
- Movie ratings.
- Basics of while loops and for loops.
- The Price Is Right game!
Lecture 7 - 9/13 - More Loops and Logical Masks
- Using a list to keep track of counts
- Using the
enumeratetype to provide a collection of indices and values to a loop - Basics of Python:Logical Masks
Lecture 8 - 9/17 - Dictionaries
- Dictionaries are collections of key : value pairs set off with { }; keys can be any immutable type (int, float, string, tuple) and must be unique; values can be any type and do not need to be unique
- Dictionary at tutorialspoint
- Storing values in a dictionary
- Bar chart demo
- Translation demo with Morse code and NATO phonetic alphabet
Lecture 9 - 9/20 - Iterative Methods
- Taylor series fundamentals
- Maclaurin series approximation for exponential uses Chapra 4.2 to compute terms in an infinite sum.
- so
- Newton Method for finding square roots uses Chapra 4.2 to iteratively solve using a mathematical map. To find \(y\) where \(y=\sqrt{x}\):
\( \begin{align} y_{init}&=1\\ y_{new}&=\frac{y_{old}+\frac{x}{y_{old}}}{2} \end{align} \) - See Python version of Fig. 4.2 and modified version of 4.2 in the Resources section of Sakai page under Chapra Pythonified
Lecture 10 - 9/24 - Binary
- Different number systems convey information in different ways.
- Roman Numerals
- Chinese Numbers
- Binary Numbers
- We went through how to convert between decimal and binary
- Floats (specifically double precision floats) are stored with a sign bit, 52 fractional bits, and 11 exponent bits. The exponent bits form a code:
- 0 (or 00000000000): the number is either 0 or a denormal
- 2047 (or 11111111111): the number is either infinite or not-a-number
- Others: the power of 2 for scientific notation is 2**(code-1023)
- The largest number is thus just *under* 2**1024 (ends up being (2-2**-52)**1024\(\approx 1.798\times 10^{308}\).
- The smallest normal number (full precision) is 2**(-1022)\(\approx 2.225\times 10^{-308}\).
- The smallest denormal number (only one significant binary digit) is 2**(-1022)/2**53 or 5e-324.
- When adding or subtracting, Python can only operate on the common significant digits - meaning the smaller number will lose precision.
- (1+1e-16)-1=0 and (1+1e-15)-1=1.1102230246251565e-15
- Avoid intermediate calculations that cause problems: if x=1.7e308,
- (x+x)/x is inf
- x/x + x/x is 2.0
- $$e^x=\lim_{n\rightarrow \infty}\left(1+\frac{x}{n}\right)^n$$
# Exponential Demo
<syntaxhighlightlang=python> import numpy as np import matplotlib.pyplot as plt
def exp_calc(x, n):
return (1 + x/n)**n
if __name__ == "__main__":
n = np.logspace(0, 17, 1000)
y = exp_calc(1, n)
fig, ax = plt.subplots(num=1, clear=True)
ax.semilogx(n, y)
fig.savefig('ExpDemoPlot1.png')
# Focus on right part
n = np.logspace(13, 16, 1000)
y = exp_calc(1, n)
fig, ax = plt.subplots(num=2, clear=True)
ax.semilogx(n, y)
fig.savefig('ExpDemoPlot2.png')
</syntaxhighlight>
- Want to see Amharic?
list(map(chr, range(4608, 4992)))
- Want to see the Greek alphabet?
for k in range(913,913+25):
print(chr(k), chr(k+32))
Lecture 11 - 9/27 - Monte Carlo Methods
- From Wikipedia: Monte Carlo method
- Walker demo
Lecture 12 - 10/1 - Matrices and Matrix Operations
- 1D arrays are neither rows nor columns - they are 1D!
- 2D arrays have...two dimensions, one of which might be 1
- Python does mathematical operations differently for 1 and 2-D arrays
- Dot products as heart of matrix multiplication
- Inner dimensions must match; outer dimensions equal dimensions of result
- To multiply matrices A and B ($$C=A\times B$$ in math or
C=A@Bin Python) using matrix multiplication, the number of columns of A must match the number of rows of B; the results will have the same number of rows as A and the same number of columns as B. Order is important - Matrix multiplication (by hand)
- Matrix multiplication (using @ in Python)
- Reformatting linear algebra expressions as matrix equations
- Calculating determinants and inverses
- Determinants of matrices and the meaning when the determinant is 0
- Shortcuts for determinants of 1x1, 2x2 and 3x3 matrices (see class notes for processes)
- $$\begin{align*} \mbox{det}([a])&=a\\ \mbox{det}\left(\begin{bmatrix}a&b\\c&d\end{bmatrix}\right)&=ad-bc\\ \mbox{det}\left(\begin{bmatrix}a&b&c\\d&e&f\\g&h&i\end{bmatrix}\right)&=aei+bfg+cdh-afh-bdi-ceg\\ \end{align*}$$
- Don't believe me? Ask Captain Matrix!
- Inverses of matrices:
- Generally, $$\mbox{inv}(A)=\frac{\mbox{cof}(A)^T}{\mbox{det}(A)}$$ there the superscript T means transpose...
- And $$\mbox{det}(A)=\sum_{i\mbox{ or }j=0}^{N-1}a_{ij}(-1)^{i+j}M_{ij}$$ for some $$j$$ or $$i$$...
- And $$M_{ij}$$ is a minor of $$A$$, specifically the determinant of the matrix that remains if you remove the $$i$$th row and $$j$$th column or, if $$A$$ is a 1x1 matrix, 1
- And $$\mbox{cof(A)}$$ is a matrix where the $$i,j$$ entry $$c_{ij}=(-1)^{i+j}M_{ij}$$
- And $$M_{ij}$$ is a minor of $$A$$, specifically the determinant of the matrix that remains if you remove the $$i$$th row and $$j$$th column or, if $$A$$ is a 1x1 matrix, 1
- And $$\mbox{det}(A)=\sum_{i\mbox{ or }j=0}^{N-1}a_{ij}(-1)^{i+j}M_{ij}$$ for some $$j$$ or $$i$$...
- Good news - for this class, you need to know how to calculate inverses of 1x1 and 2x2 matrices only:
- Generally, $$\mbox{inv}(A)=\frac{\mbox{cof}(A)^T}{\mbox{det}(A)}$$ there the superscript T means transpose...
- $$ \begin{align} \mbox{inv}([a])&=\frac{1}{a}\\ \mbox{inv}\left(\begin{bmatrix}a&b\\c&d\end{bmatrix}\right)&=\frac{\begin{bmatrix}d &-b\\-c &a\end{bmatrix}}{ad-bc} \end{align}$$
Lecture 13 - 10/18 - Office Hours
- Office Hours
Lecture 14 - 10/11 - Norms and Condition Numbers
- Chapra 11.2.1 for norms
- np.linalg.norm() in Python
- Chapra 11.2.2 for condition numbers
- np.linalg.cond() in Python
- Note: base-10 logarithm of condition number gives number of digits of precision possibly lost due to system geometry and scaling (top of p. 295 in Chapra)
Lecture 15 - 10/15 - 3D Plotting
- subplots
- Python:Plotting Surfaces
Lecture 16 - 10/18 - Statistics and Curve Fitting I
- Definition of curve fitting versus interpolation:
- Curve fitting involves taking a scientifically vetted model, finding the best coefficients, and making predictions based on the model. The model may not perfectly hit any of the actual data points.
- Interpolation involves making a guess for values between data points. Interpolants actually hit all the data points but may have no scientific validity at all. Interpolation is basically "connecting the dots," which may involve mathematically complex formulae.
- Statistical definitions used (see Statistics Symbols for full list):
- $$x$$ will be used for independent data
- $$y$$ will be used for dependent data
- $$\bar{x}$$ and $$\bar{y}$$ will be used for the averages of the $$x$$ and $$y$$ sets
- $$\hat{y}_k$$ will be used for the estimate of the $$k$$th dependent point
- $$S_t=\sum_k\left(y_k-\bar{y}\right)^2$$ is the sum of the squares of the data residuals and gives a measure of the spread of the data though any given value can mean several different things for a data set. It will be a non-negative number; a value of 0 implies all the $$y$$ values are the same.
- $$S_r=\sum_k\left(y_k-\hat{y}_k\right)^2$$ is the sum of the squares of the estimate residuals and gives a measure of the collective distance between the data points and the model equation for the data points. It will be a non-negative number; a value of 0 implies all the estimates are mathematically perfectly predicted by the model.
- $$r^2=\frac{S_t-S_r}{S_t}=1-\frac{S_r}{S_t}$$ is the coefficient of determination; it is a normalized value that gives information about how well a model predicts the data. An $$r^2$$ value of 1 means the model perfectly predicted every value in the data set. A value of 0 means the model does as well as having picked the average. A negative value means the model is worse than merely picking the average.
- Mathematical proof of solution to General Linear Regression
- Python:Fitting
Lecture 17 - 10/22 - Statistics and Curve Fitting II
- Linear versus Nonlinear Fits
- Clarification on how general linear regression works
Lecture 18 - 10/25 - Statistics and Curve Fitting III
- Walkthrough of a general linear fit
- args in function definitions and their usefulness
- Non-linear models
- Python:Fitting#Nonlinear_Regression
Lecture 19 - 10/29 - Finding Roots
- Python:Finding roots
- SciPy references (all from Optimization and root finding):
- scipy.optimize.brentq - closed method root finding
- scipy.optimize.fsolve - open method root finding
Lecture 20 - 11/1 - Finding Extrema
- Python:Extrema
- SciPy references (all from Optimization and root finding):
- scipy.optimize.fmin - unbounded minimization
- scipy.optimize.fminbound - bounded minimization
Lecture 21 - 11/5 - Interpolation
- Python:Interpolation
- Interpolations are meant to estimate values between points in a data set.
- Interpolants must go through all the data points - different concept from a fit; also interpolation functions generally have different coefficients for the interpolant between every pair of points - very different from a fit
- Unlike a model, the functions used to interpolate may have no scientific validity; instead, they satisfy different mathematical conditions.
- The main interpolations we looked at are nearest neighbor, linear, and cubic spline with different conditions (not-a-knot, clamped, natural)
- Most basic interpolation simply looks at most recent value of data (i.e. data point "to the left")
- Next most basic is nearest neighbor - closest point
- Next is linear interpolation - straight line between neighboring points
- After that, using third-order polynomials is common
Lecture 22 - 11/8 - Zips, Maps, and Filters
- Maps, filters, zips create a one-time-use iterable type
- map(FUN, ITERABLE) applies a function to each element in an iterable and returns an iterable
- filter(FUN, ITERABLE) applies a logical expression to each element and includes that element in the return only if the function is true
- zip(A, B) takes corresponding elements from A and B and returns an iterable made up of tuples with the corresponding elements from A and B
- Very useful for making a dictionary out of a collection of keys and a collection of values
- List comprehensions
- [FUNCTION for VAR in SEQUENCE if LOGIC]
- The FUNCTION should return a single thing (though that thing can be a list, tuple, etc)
- The "if LOGIC" part is optional
[k for k in range(3)]creates[0, 1, 2][k**2 for k in range (5, 8)]creates[25, 36, 49][k for k in 'hello' if k<'i']creates['h', 'e'][(k,k**2) for k in range(11) if k%3==2]creates[(2, 4), (5, 25), (8, 64)]
- [FUNCTION for VAR in SEQUENCE if LOGIC]
- Scrabble example
Lecture 23 - 11/12 - Class Cancelled
Lecture 24 - 11/15 - Numerical Integartion and Differentiation I
- Newton Interpolating Polynomials
- Overview of integration
- Riemann sums
- Trapezoidal Rule
- Simpson's 1/3 and 3/8 Rules
- Overview of differentiation
- 2pt forward first derivative
- Exception at first point
- 2 pt backward first derivative
- Exception at last point
- 3pt centered first derivative
- Exceptions at first and last points
- 3pt centered second derivative
- Exceptions at first and last points
- 2pt forward first derivative
Lecture 25 - 11/9 - Numerical Integartion and Differentiation II
- Working examples by hand
- Writing code for some of the above
Lecture 26 - 11/22 - Office Hours
Lecture 27 - 11/29 - Initial Value Problems
- Introduction to IVP where $$\frac{dy}{dt}=f(t, y, C)$$ and $$y_0$$ is known
- Overview of particular and homogeneous solutions
- Euler-Cauchy method
- Runge-Kutta 4
- Python:Ordinary Differential Equations